範囲と平均値に注目して資料を分析する。 ・ 資料の範囲を求め,読み取れることを考えさせる。 ・ 2つの分布の異なる資料について平均値を求めさせ, そこから考えられることを考えさせる。 ・ 外れ値を取る資料を取り扱 うことで,平均値を代表値と3 代表値(平均値,中央値,最頻値) 2時間 4 資料の活用(資料の活用,コンピュータを用いた統計処理) 3時間 (本時3/3) 5 近似値の有効数字(近似値,真の値,有効数字) 1時間 6 学習のまとめ第1学年 7 資料の活用 数学的な思考力・判断力・表現力を育む問題解答 年 組 号 氏名 練習問題③ (1) 0 m以上250 m未満の階級 ポイント 中央値は,大きい順に並べた中央の値だね。 この資料は偶数だから,25 番目と26 番目

中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ
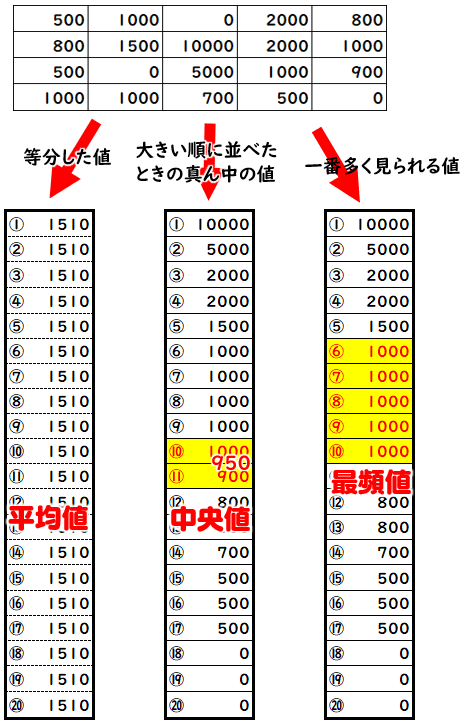
資料の活用 平均値と中央値
資料の活用 平均値と中央値-平均値= {(階級値)×(度数)}の合計 度数の合計 = 960 =48 (cm) 答 48 cm 考え方 45 cm 以上 50 cm 未満の階級値 47 5 cm を仮の平均とする。 平均値=仮の平均+ {(階級値-仮の平均)×(度数)}の合計 度数の合計 解き方 475+元でも活用できる資料内容であること。 ③ 具体的な発問や投げかけの形に表現して、「すぐに使える」資料として活用できるようにすること。 ④ ビジュアル化をり 、短時間で授業のポイントをつかむことができるようにすること。 平均値の妥当性は



資料の活用の問題で 中央値 最頻値 平均値の3つの問題の解き方教えて Yahoo 知恵袋
イ ヒストグラムや代表値を用いて資料の傾向をとらえ説明すること。 〔用語・記号〕 平均値 中央値 最頻値 相対度数 範囲 階級 内容の取扱い (6) 内容の「D資料の活用」の(1)に関連して,誤差や近似値,a×10n の形の表現を取り扱 うものとする。・あれ,平均値が じなのにおかしい。 ・売れた弁当の値段や個数を詳しく知りたい。 2 データを分析し,c店が売れなかった理由を考 える。 (分) ・b店は平均値と最頻値,中央値が じ場所にある。 ・c店は平均値と最頻値,中央値が じ場所にない。資料の活用 代表値(1) 175 範 囲資料全体の散らばり具合を表す数値のこと。 (範囲)=(最大の値)-(最小の値) 代表値資料全体の特徴を、1つの数値で表したもの。 ・平均値 個々の資料の値の合計を、資料の総数でわったもの。
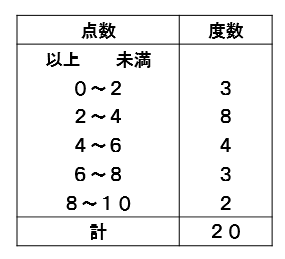
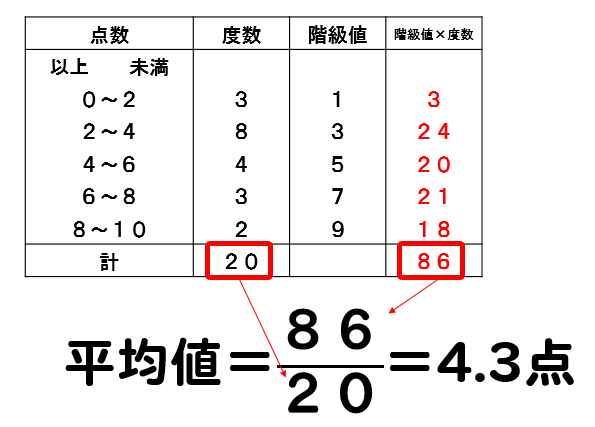
D 資料の活用 ⑴ イ 学習指導要領における領域・内容 課題の見られた問題の概要と結果 あれ?平均値なのに245 cmの あたりがへこんでいるよ。 そうだね。230 cmも高いよ。 グラフには2つの山があ平均値: 個々の資料の値の合計を資料の総数で割った値 もう一つが、度数分布表から平均値を求める求め方です。 度数分布表からも平均値を求めることができます。 計算の仕方は下記のとおりです。 1、各階級の階級値を求める。 2、その各階級値に各平均値 (資料の個々の値の合計 )÷(資料の個数) 1年「資料の活用」① 氏名 1 下の表は、ある中学校の男子生徒40人の身長の測定結果をまとめたものです。 ⑴ 階級の幅を答えなさい。 ⑵ 最頻値を求めな
ウ②問題を解決するため,平均値や中央値 や最頻値を求めることができる。 資料の範囲や最大値・最小値 について理解したり,資料を 度数分布表に整理したりし て,分布の様子を調べる。 (1) エ②代表値の必要性と意味を理解してい る。数学 類題にチャレンジ 〔資料の活用〕 資料の活用 語句のまとめ ア 平均値は19mより小さい。 イ 中央値含まれている階級の相対度数は02 より小さい。 ウ 階級の幅は3m である。 エ ボール投げの記録の分布の範囲は16mより大きい。1 年 資料の活用 「貧困率」を改善するには ~国民生活基礎調査のデータの分布傾向から考える~ 分布の形・代表値(平均値・中央値・最頻値)・ヒストグラム 1.問題について 平成21 年10 月 日の新聞に以下の記事が掲載された。




中学1年生 数学 資料の整理 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



資料の活用 Qikeru 学びを楽しくわかりやすく
(2)「資料の活用」領域の目標について すると,例えば100 人の生徒のハンドボール投 げの記録を取る場合,この100 人の記録の平均値を求めることを目的だと考えれば,それまでであ〔用語・記号〕平均値 中央値 最頻値 相対度数 範囲 階級 目的に応じて資料を収集し,統計的な処理を行うことによって傾向をよみ取り,説明することの中でも,1年の学習では,文字通り「資料の活用方法」を学ぶことになる。量関係」や中学校「資料の活用」を,小中学 校ともに「データの活用」と統一した。さら に,内容の移行については,小学校第6学年 では,平均値,中央値,最頻値などの代表値 について,中学校では,新規に指導する内容




2 Dfracdfrac150 1 Descubre Como Resolverlo En Qanda




中1 数学 中1 87 代表値と散らばり Youtube
代表値・平均値 引き続き「資料の整理」です。 使い慣れない言葉の意味さえ覚えれば、あとは難しいことはありません。 確実に得点源にしましょう。 範囲 資料の最大から最小を引いた値を 範囲といいます。 例 生徒 \(8\)資料の測定 世の中には様々な統計資料がある。ここではどのようにまとめられているかを見て行こう。 近似値 たとえば、エンピツの長さを 定規 (じょうぎ) で測定してみて、測定値が 85cmという結果だとしても、 そのエンピツの長さは、851cmかもしれないし、cmかもしれないし1 題材 「資料の活用~資料の散らばりと代表値~」 2 題材について 平成24年度より完全実施となる新学習指導要領で、新たに1つの領域として設けられたの が「D資料の活用」である。本題材は、この「D資料の活用」領域の1学年の学習内容とし



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ



代表値 平均値 中央値 最頻値 の意味と違い 数学fun
・階級値 ⑤個々の値がわからない資料における代表値の求め方を知る。 ㋑ ㋑ 6 ⑥代表値Ⅲ ・範囲 ⑥資料のばらつき程度を表す値があることを知る。 ㋑ ㋑ 7 ㋐ ⑦統計資料の 活用Ⅰ ⑦統計的手法を活用して,問題を解決する。 ㋑(4) 資料の平均や散らばりを調べ、統計的に考察したり表現したりすることができるようにする。 ア 資料の平均について知ること。 イ 度数分布を表す表やグラフについて知ること。 第5学年では、測定値としての平均について扱い、その意味や求め方を第1学年 7 資料の活用 知識・技能の習得を図る問題 年 組 号 氏名 練習問題④ 1 1500 mが次の位までの測定値のとき,この測定値を有効数字で表しなさい。 3(m)と表す



無料 中1数学 発展問題 問題プリント 資料の活用2 平均 相関



1
て,資料の傾向を読み取り,説明するこ とができる。 2 代表値と散らばり(3) ・問題を解決するため,平均値を求めるこ とができる。 ・代表値の必要性と意味を理解している。 ・平均値を用いて資料の傾向を調べ説明し ようとしている。 行動観察キーワード 新学習指導要領,中学校数学,資料の活用,度数分布表,代表値,有効桁,10n 1 はじめに 平成24年度に実施される中学校の新学習指導要領4 の数学では,従来の領域「数量関係」が2つに分かれて, 新領域は「数と式」,「図形」,「関数」,「資料の活用」中学1年生 数学 資料の活用近似値と有効数字 練習問題プリント 無料ダウンロード・印刷 中学1年生 数学 空間図形立体の体積と表面積 練習プリント 無料ダウンロード・印刷 中学1年生 数学 空間図形立体の表し方 練習プリント 無料



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ



1
第4部 さまざまな統計データをいかに活用するか ~その1~ 集めたデータを整理しよう。(中1の「資料の活用」の学習が役に立ちます) 整理の仕方の例 ・度数分布表にまとめ、ヒストグラムに表す。 ・平均値や最頻値など代表値を求める。 3.正規分布の基本性質 ① 正規分布の形は平均値と標準偏差で決まる ② 平均値と最頻値と中央値が一致する ③ 3σでデータを管理できる(図2) 4.品質管理(QC)での活用 (1)特定数値データの確率を予測する (2)データの管理上限と下限値を決める 最頻値(モード)の求め方 を知っていると便利。 資料と活用の問題がとけるし、 日常生活でもつかえるようになるんだ。 今日はそんな便利な、 最頻値(モード)の求め方 を2ステップで解説していくよ。 よかったら参考にしてみてね^^



中1数学 発展 応用問題プリント 資料の活用1 度数分布表 144




度数分布表から平均値を求める 中学1年の数学 身勝手な主張
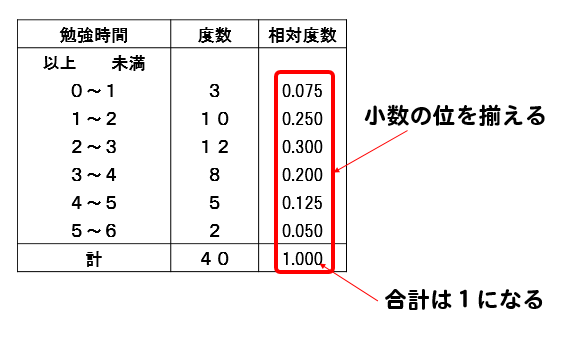
度数分布表における平均値、度数、相対度数の求め方を理解しておく。 数学用語(平均値、中央値、最頻値、階級、相対度数、幅)の理解。 度数分布表を用いた問題の出題が最も多い。 他県では、2つのヒストグラムや度数分布表の比較の問題が多く出題されています。 7章資料の活用p17章 資料の活用 2年 組 番名前 ルーラーキャッチって、どんな遊び??? 落下する定規を何㎝のところでつかめるのか?を調べる遊びです。 →詳しくは、1年生の教科書232ページを見てね! 1.まずは、平均値で比べてみましょう。 代表値としての平均について理解する。 評価規準 資料の特徴を調べる時に、平均を用いることがあることを理解している。(知識・理解) 問題 12 月10 日に、重い卵がよく産まれたと言えるのは、東小屋と西小屋のどちらの小屋ですか。




資料の整理 平均値 中央値 Youtube




平均値 中1数学 資料の活用3 Youtube
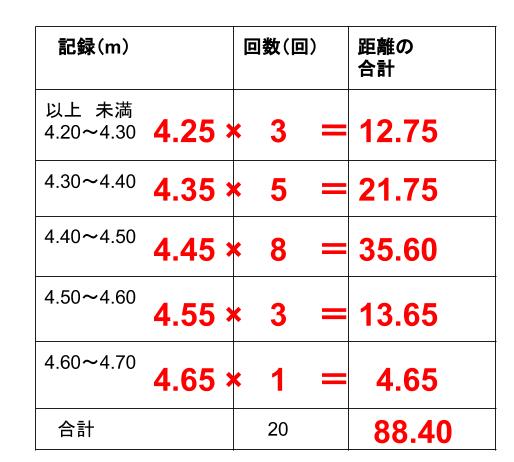
平均値と答える生徒は 「31人のデータを集めたカツオは平均 予想される意見 多い。そこで,平均値 値を計算しました。すると65円で・平均値は外れ値の影響を受け は65円であり,小遣 す。母親は平均を根拠に00円でい る。 いをあげる根拠にならタからグラフなどを作成したり、平均を求め たりしておく。 平均値だけでは資料の傾向を読み取ること ができないことに気付かせるために、平均値 が等しい二つの資料のグラフの形に違いが表 れるように数値を意図的に調整する。平均値を求めよ。 平均値= 値の合計 資料の総数 度数分布表から平均を求める場合、各階級の資料の値はすべて階級値として計算する。 計算(1475×××××2)÷=1565 中央値を求めよ。 中央値とは資料を大きさの順に並べたときのちょうど




中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ



1
数学17章データの分布「ヒストグラムや代表値の意味」<基本問題①> (令和3年度以降は小学校6年の内容の復習として活用ください。 組 番 名前 1次の2つの表は,ある中学校1年生人のテスト前日の家庭学習時間を,グループAと



資料の活用の問題で 中央値 最頻値 平均値の3つの問題の解き方教えて Yahoo 知恵袋




中1数学 資料の活用 平均値の求め方 Youtube




中1数学 相対度数の求め方 例題編 映像授業のtry It トライイット
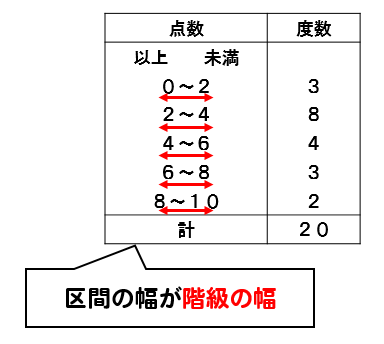



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ
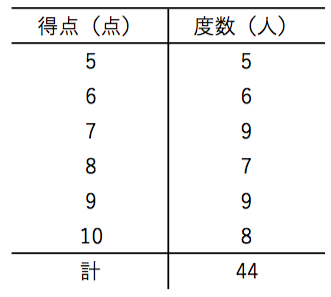



平均値について 苦手な数学を簡単に




中学1年生 数学 資料の整理 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
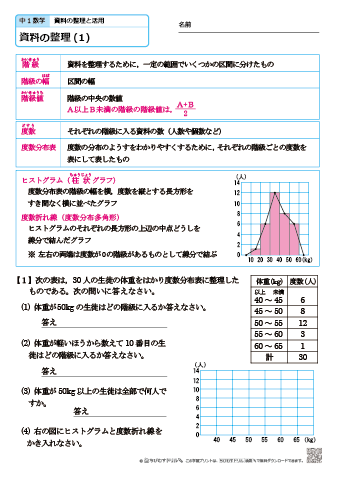



中学1年生 数学 資料の整理 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




世界一わかりやすい数学問題集中1 7章 資料の活用



Www Chuo Tky Ed Jp Ginza Jh Resources Content 0513 Pdf
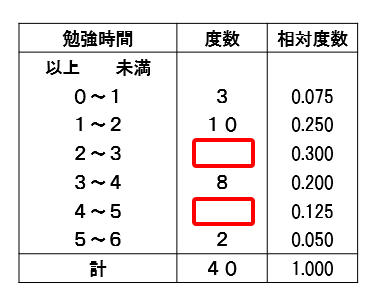



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ




平均値と階級値について 苦手な数学を簡単に



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ
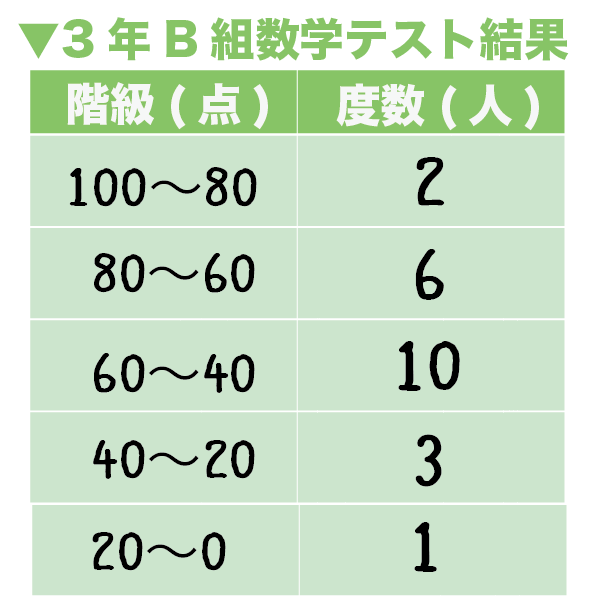



度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




資料の活用 用語 基本のまとめと演習問題 中学生 数学のノート Clear




2 解答見ても分からないので教えてください Clear
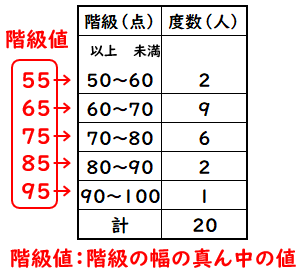



代表値 平均値 中央値 最頻値 の意味と違い 数学fun



中学校数学 資料の活用 で学ぶ 中央値について質問です 資料が Yahoo 知恵袋



資料の活用 まとめ2 中学から数学だいすき



Http Www Pref Osaka Lg Jp Attach 6629 Jmw 1d7 3 Pdf




度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




中1数学 資料の活用 の重要ポイントをピックアップし 勉強方法を紹介 札幌市 西区 琴似 発寒 塾 学習塾 個別指導塾 マナビバ




中学数学 資料の散らばりと代表値




度数分布表から平均値を求める 中学1年の数学 身勝手な主張



Www Nichibun G Co Jp Library E Other C Sugaku Data Katsuyou Shido Pdf



Http Ed City Daito Osaka Jp Weblog Files Tani Jhs Doc 7965 Pdf




中1数学 資料の活用のポイント練習問題
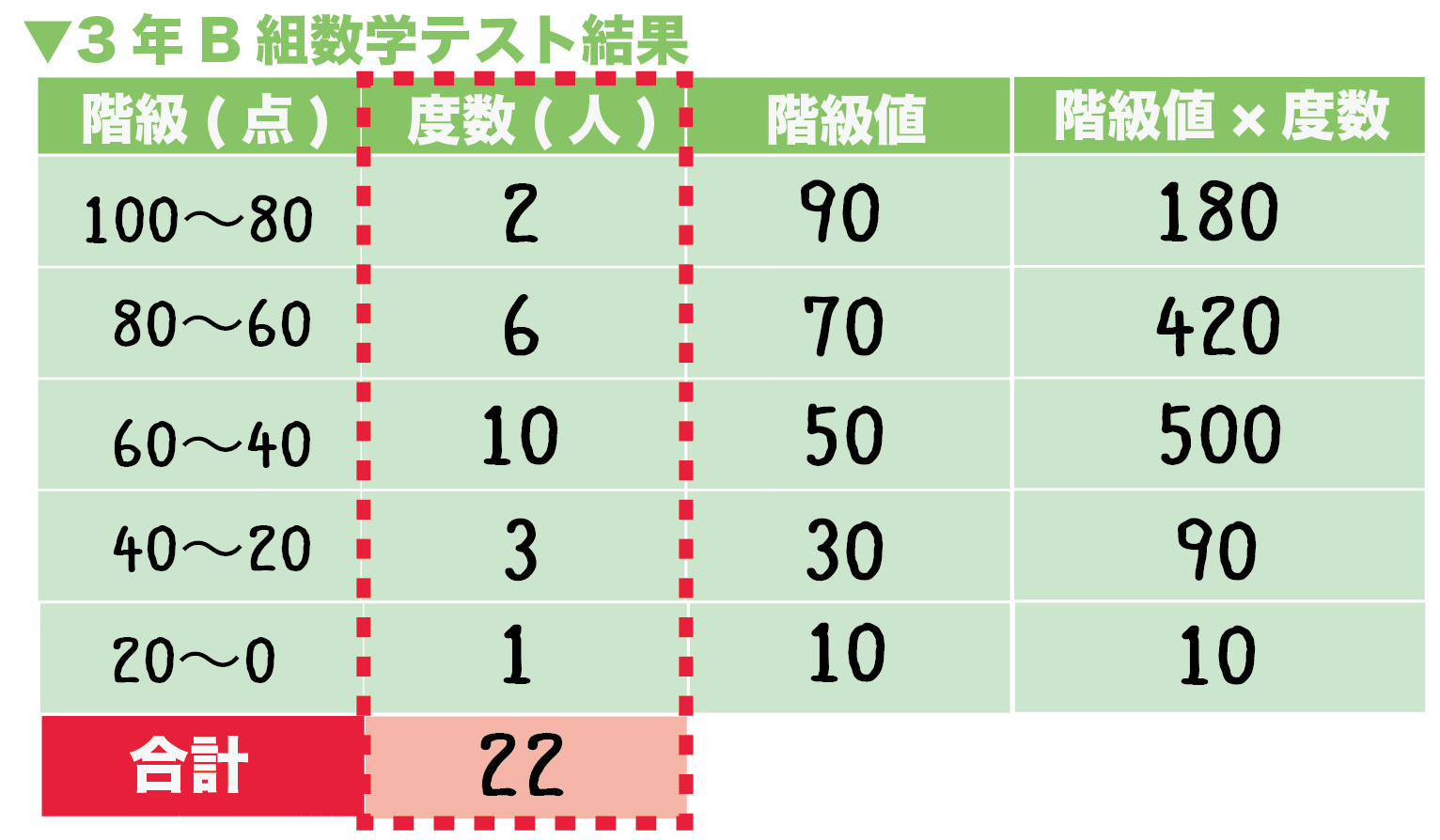



度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




中3の実テ過去問の 資料の活用についての問題です Clear




世界四季報 日本人の寿命の 平均値 と 中央値 と 最頻値 16年 男性の場合 平均値 81歳 中央値 歳 最頻 値 87歳 女性の場合 平均値 87歳 中央値 歳 最頻値 93歳 T Co R4nrglo12l T Co 0tlkwso0qr




代表値 平均値 中央値 最頻値 の意味と違い 数学fun




中1数学 平均値 と 中央値 練習編 映像授業のtry It トライイット




中3数学夏休み 16 資料の活用 度数分布表から平均値を求める問題 中3生用夏休みの重要問題の解説授業動画 Youtube



1



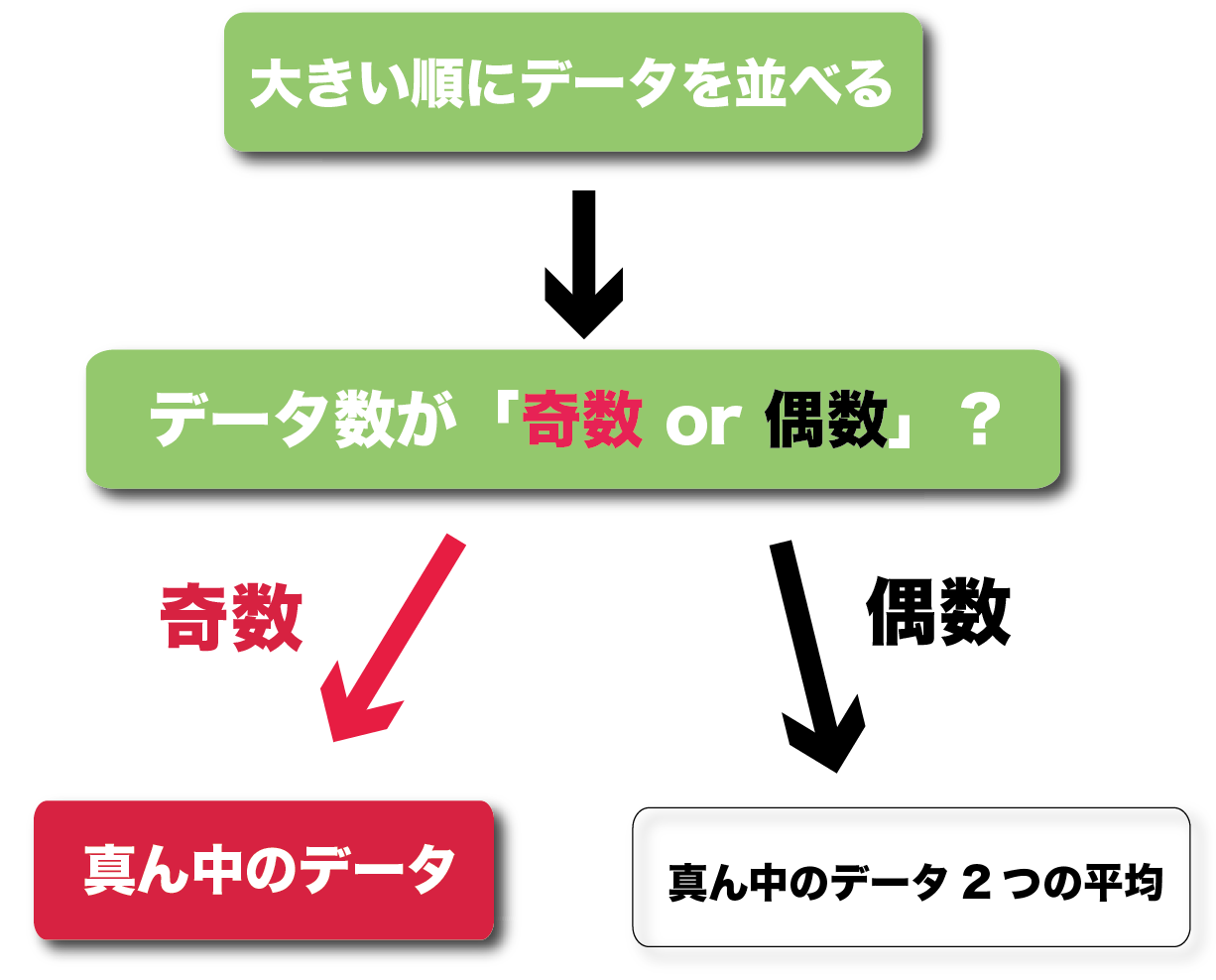
中1数学 中央値の求め方はこれでバッチリ 偶数 奇数の場合をそれぞれ解説 数スタ
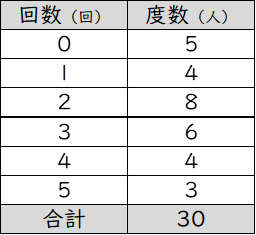



中1数学 資料の整理のポイントと定期テスト予想問題 Pikuu




小学6年生の算数 資料の調べ方 度数分布表 柱状グラフ 練習問題プリント ちびむすドリル 小学生




中学数学 資料の分析と活用 資料の整理 問題まとめ集 全国公立高校過去問解説集 わかりやすさに徹底的にこだわっています 教育 学習 受験 自宅でできる受験対策ショップ ワカルー Wakaru




受験対策 数学 資料の活用 Youtube
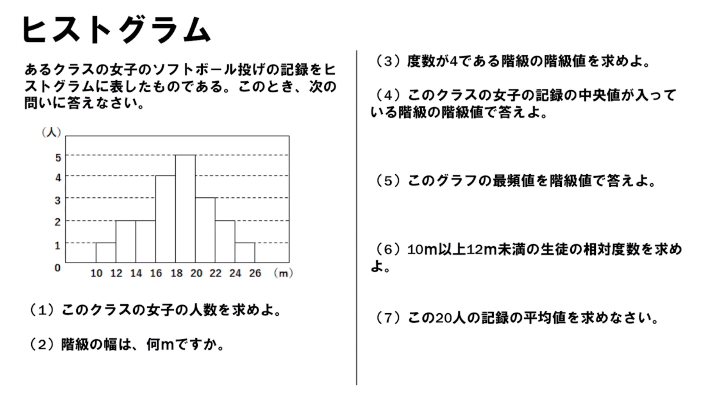



中1数学 資料の整理のポイントと定期テスト予想問題 Pikuu




中1 数学 資料の分析と活用のヒストグラムのところです 答えは 1 イ ウ Clear
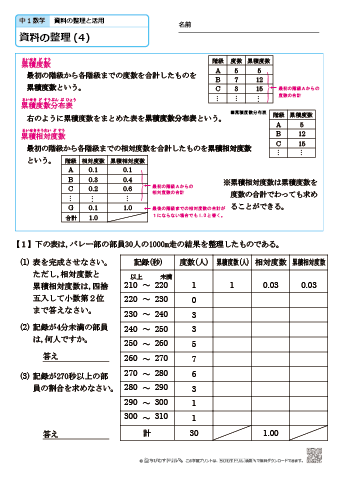



中学1年生 数学 資料の整理 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学数学 資料の散らばりと代表値




中1数学 資料の整理のポイントと定期テスト予想問題 Pikuu



代表値の応用問題 教遊者



中学数学 代表値 平均値 中学数学の無料オンライン学習サイトchu Su




度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ




全国学力調査 埼玉県の中3ができない数学の内容は 2 ブログ アビット



Saiei School Com Wp Content Uploads 16 12 Teretama Math Ruidai Pdf




代表値と散らばり 数学の要点まとめ 練習問題一覧



無料 中1数学 標準問題 解答プリント 145 資料の活用2 近似値



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ




代表値の応用問題 教遊者



度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく



Http Toro J Saitama City Ed Jp Kadai 2nenn Kyouka 2suugaku 2nennsiryou3 Pdf




中学数学 中央値 メジアン の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



2




中学数学 資料の散らばりと代表値




相対度数の意味と計算方法 数学fun




中1 数学 資料の整理4 平均値と中央値 12分 Youtube




代表値の応用問題 教遊者




中学数学 資料の散らばりと代表値




中学数学 資料の散らばりと代表値




7章資料の活用10 度数分布表と平均値 中学校1年生の数学を教科書 啓林館 にそって学習しよう Youtube



2



中学校数学 資料の活用 で学ぶ 中央値について質問です 資料が Yahoo 知恵袋
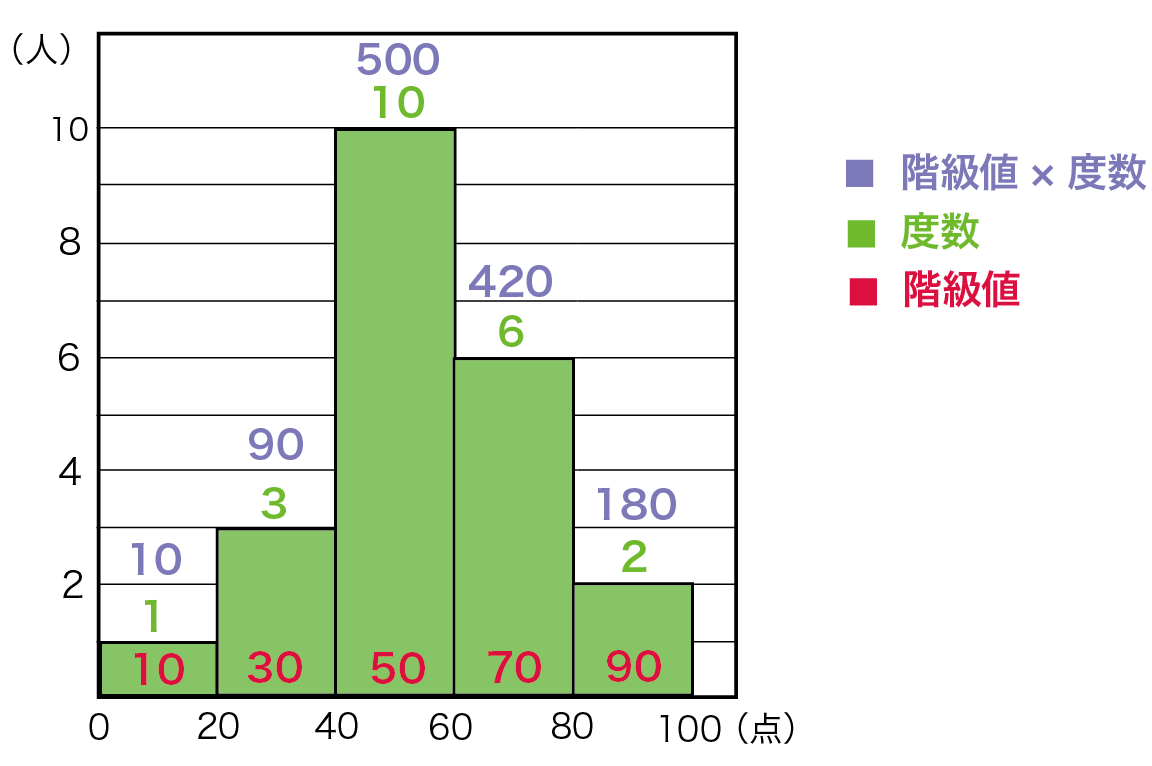



ヒストグラムを使った平均値の求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
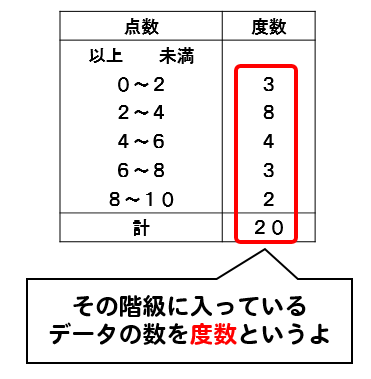



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ



至急 数学の資料の活用で質問です 下の図で 6 5秒以上7 0秒未満の階 Yahoo 知恵袋



無料 中1数学 基本解説 解答プリント 資料の活用2 近似値 145




國一 Junior High数学的数学 7章 資料の分析と活用 筆記 Clear




高校受験対策 資料の活用 最頻値と平均値 の問題 動画 19ch
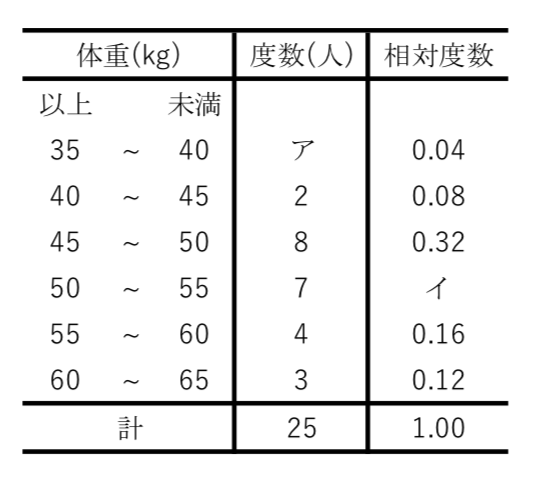



度数分布表を完成させよう 求め方は決まっている 苦手な数学を簡単に
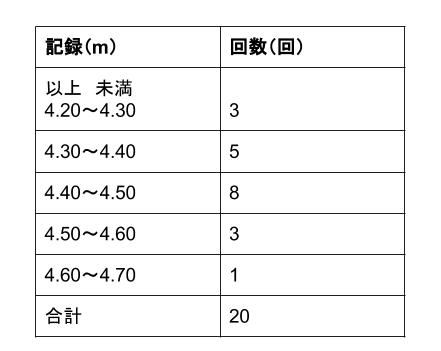



中学数学 代表値 平均値 中学数学の無料オンライン学習サイトchu Su




連立方程式 平均に関する問題 その1 N Kaneta Blog
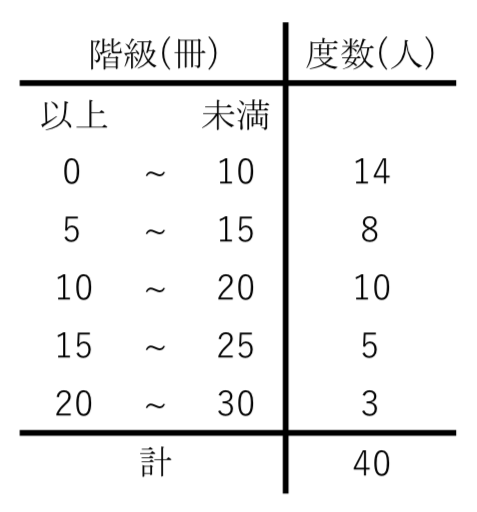



度数分布表から相対度数を求める 苦手な数学を簡単に




中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ




5 P 147kmh 105km Descubre Como Resolverlo En Qanda




中1数学 資料の活用 平均値の求め方 Youtube




中1数学 資料の散らばりと代表値 まとめ 中学生 数学のノート Clear
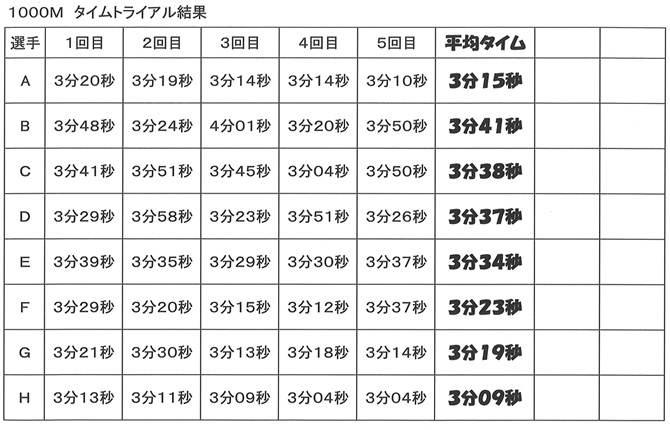



授業実践記録 数学 資料の活用 啓林館



資料整理の用語 中学から数学だいすき




資料のちらばりと代表値 度数分布表からの平均値の求め方 中学数学 定期テスト対策サイト




中1 数字 資料の活用 絶対攻略 中学生 数学のノート Clear




度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく
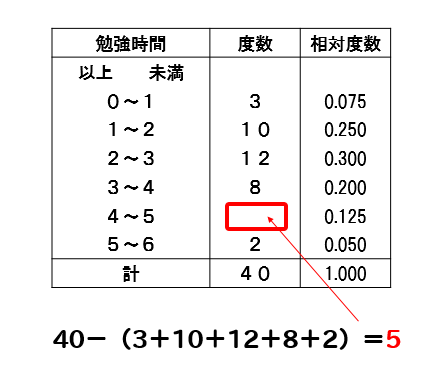



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ
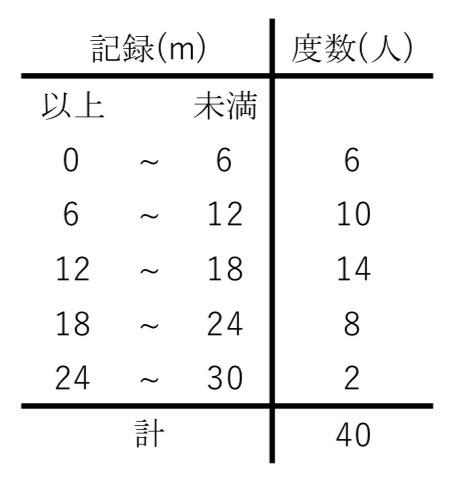



度数分布表から平均値と最頻値を求める 苦手な数学を簡単に



0 件のコメント:
コメントを投稿