平行四辺形の面積求めます のアンケート記入欄 平行四辺形の面積を求めるプログラムです 本ライブラリは会員の方が作成した作品です。 内容について当サイトは一切関知しません。平行四辺形の面積 まず, 2つのベクトル ベクトルを横に書く悪習は辞めましょう が張る平行四辺形の面積 を考えよう 平行四辺形 abcd がある。 違う位置にあっても、「向き」と「大きさ」が同じであれば、同じベクトルであるとされます。今回は平行四辺形の角度、辺の長さの求め方について解説していくよ! 平行四辺形の性質を覚えておけば 簡単に解ける問題ばかりだから 今回の記事でしっかりとマスターしていこう!

高校数学 平行四辺形の面積の求め方 練習編 映像授業のtry It トライイット
平行四辺形の面積の求め方 ベクトル
平行四辺形の面積の求め方 ベクトル- ベクトルの外積 (裏技)による法線ベクトル・空間の三角形の面積・平行六面体の体積・四面体の体積 ベクトルの外積は受験数学最強の裏技の1つであり,\ 上級者は是非習得しておいてほしい 大学1年の最初に学習する程度の知識であり,\ 適用できる試験問題 高校 数学 物理 ベクトル 平行四辺形 a(1,2,3) b(3,2,1)の平行四辺形の面積の求め方を教えて欲しいです。 数学 内積の定義式をあのように定義する必要があったのはなぜですか?



Excelを使った数値計算ツールsuitexl
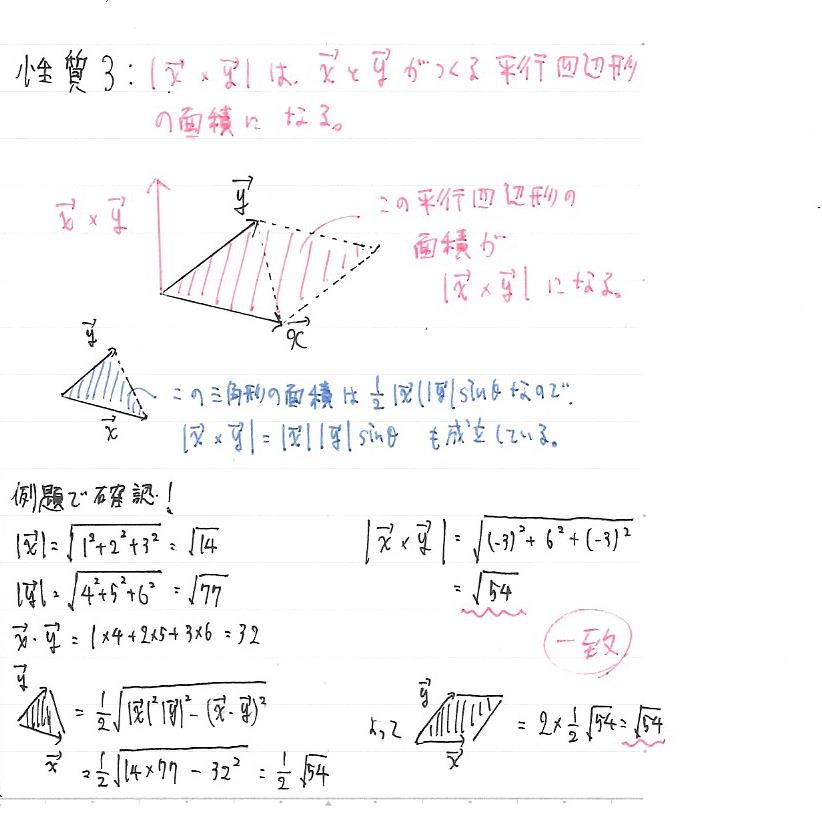
2 面積と体積 21 平行四辺形の面積 n 次元ベクトルa,b の作る平行四辺形(右下図) の面積をS とすれば, a,b のなす角をθ (0 ď θ ď π) として, S2 " p∥a∥∥b∥sinθq2 " ∥a∥2∥b∥2! なんと、元々の2本のベクトルが作る平行四辺形の面積になるのです!! 外積を使った入試問題の例 では、これを使うとどのように便利なのか。 実際の入試問題でも確認できます。 例えばこの問題。 東京大学14年 理系第1問証明 はじめに 3次元ベクトル空間の任意のベクトルは、 3つの線形独立なベクトルによる線形結合によって表すことができる (「次元と同じ数だけある線形独立なベクトルは基底になる」を参考) 。 従って、 $0$ でない2つの線形独立なベクトル $\mathbf{a}$, $\mathbf{b}$ とそれらの間の外積
数学切り抜き帳 このタイトルを見て「こんなこと誰でも知っているのに」と思う読者もいるに違いない, 確かに面積の求め方は誰でも知っている.しかし,この求め方(計算法)の根底にあるものを 高校生の目で 見直してもらいたい. 平行四辺形の(1)空間において,2つのベクトルα,あを2辺とする平行四辺形の面積をぶとすると, (新潟大) β=石油毎-(孟・毎であることを示せ。 (2)乃を整数とし,2つのベクトル;=(乃,0,1),∂=(0,乃+1,1)を2辺とする平行四辺形の面 積を品 とする。 (6) 平行四辺形の面積・平行六面体の体積 外積を用いることで、ベクトルが張る平行四辺形の面積、ベクトルが張る平行六面体の体積を求めることができます。 (i) 平行四辺形の面積 2つのベクトル \( \vec{a} \), \( \vec{b} \) が張る平行四辺形の面積 \( S \) は\
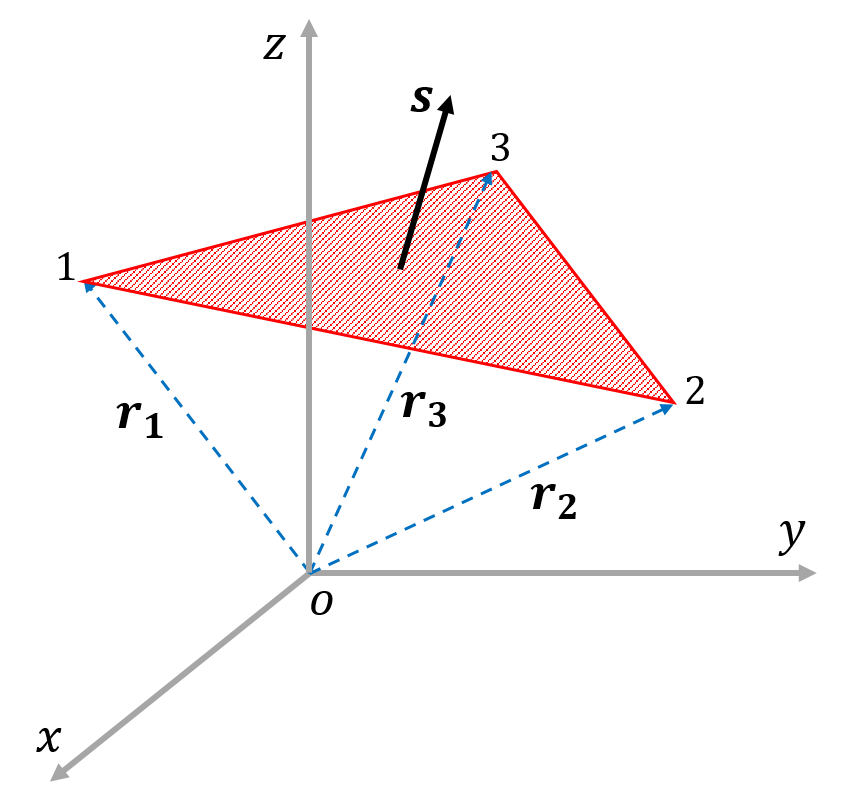
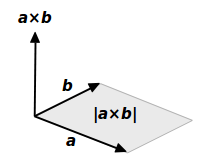
平面の法線ベクトル a&b& の長さは、平行四辺形の面積 u S に等しい b & a & S ab && u a,b & が作る平行四辺形を含む面に 垂直で、長さが1のベクトルを法線ベク トルといい、 a b a b S a b 空間において平行四辺形や三角形の面積を求めるとき 外積の大きさは2ベクトルによって作られる平行四辺形の面積に等しい ので、外積ベクトルを求めてからその大きさを求めることによって 平行四辺形やそれを対角線で切った三角形の面積を求めるのに役立ちます 。 ただ、2つのベクトルによってできる三角形の面積を求める場合には、O, A(a), B(b), C(ab) は平行四辺形となる. ⁄ 注意 116 (ベクトルのスカラー倍) ベクトル a とそのスカラー倍 b = αa を考える. 点 A ( a ), B ( b ) とする.このとき点 B は直線 OA 上にある.線分 OB の長さは線分 OA の長




物理のための数学 ベクトルの外積 お茶処やまと屋




勉強しよう数学3c エディントンのイプシロンと行列式とベクトルの外積
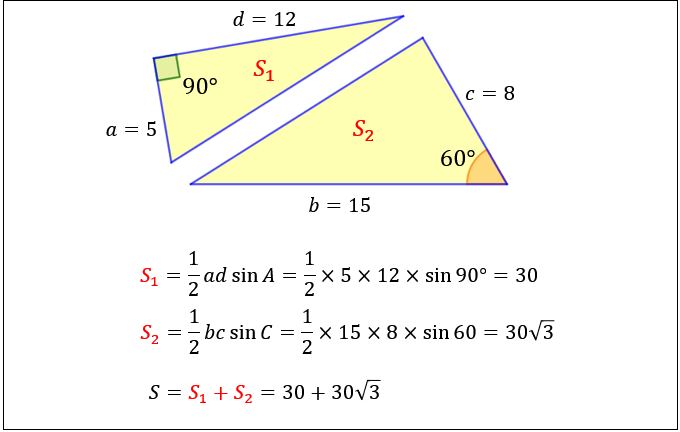
G36 平行四辺形の面積(空間の場合) ベクトル a =(a 1 ,a 2 ,a 3 ) と b =(b 1 ,b 2 ,b 3 ) が作る平行四辺形の面積 S は次の式で 与えられる。ここでは ベクトル積 (クロス積、外積) の大きさは、2 つのベクトルが作る平行四辺形の面積に等しい ということについて説明します。 以前の説明 ではベクトル a → \overrightarrow {a} a と b → \overrightarrow {b} b が張る平行四辺形に、 そっと ∥ a → × b 四角形の4つの辺の長さ a, b, c, d に加え、どちらか一方の対角線の長さ e が分かっている場合。 四角形を2つの三角形に分けてから各三角形の面積 S 1, S 2 を ヘロンの公式 を使って求め、それらを合計することで四角形の面積を求めることができます。
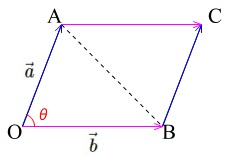



ベクトルの大きさと内積だけで表す面積の公式




高校数学 平行四辺形の面積の求め方 例題編 映像授業のtry It トライイット
ベクトルの外積と平行四辺形の面積 (18年8月日) では、向かい合う2つのベクトルを一辺とする平行四辺形の面積の求め方を取り上げた。方法としては ①2つのベクトルの内積を使う方法(高校数学また平行四辺形OAGDの面積と長方形OAG'D'の面積は等しい。つまり が成り立つ。 このときπ平面上のベクトルの方向に関して であることが言える。 このことと、||:||=OB':OC' であることを考慮すると、平行四辺形OB'D'C'と平四辺形OHJIは互いに1´ ´ a¨b ∥a∥∥b∥ ¯2) " ∥a∥2∥b∥2 ´pa¨bq2 " ˆÿn i"1 a2 i ˙ˆÿn j"1 b2 j
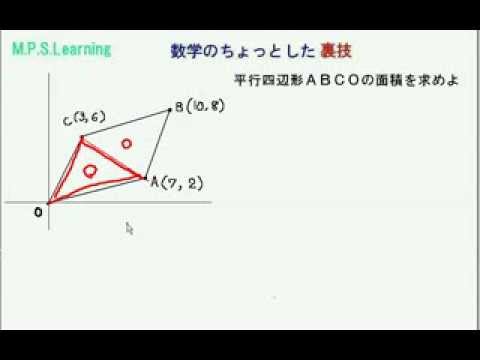



1次関数の応用 平行四辺形の面積 Youtube
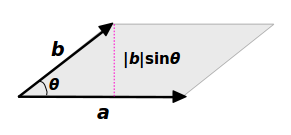



ベクトル積の大きさは平行四辺形の面積 ベクトル解析 基礎からの数学入門
2ab\,の成分は,\ x成分とy成分を別々に計算するだけである 大きさは\ √8^24^2}=√80}=4√5\ と計算してもよいが,\ うまくない 今後z成分も考慮したり,\ 数値が大きくなったりした場合,\ 計算が一気に面倒になる 2ab= (8,\ 4)=4 (2,\ 1)と考えると,\ 実質的に\ √2^21^2X と y が同じ長さのベクトルである場合、polyarea は、x と y によって定義された多角形のスカラーの面積を返します。 x と y が同じサイズの行列である場合、polyarea は、x と y の列基準のペアで定義された各多角形の面積を含む行ベクトルを返します。 x と y が多次元配列である場合、polyarea は平行四辺形の面積 = 底辺 ×高さ = 5× 12 = 60cm2 平行四辺形の面積 = 底辺 × 高さ = 5 × 12 = 60 cm 2
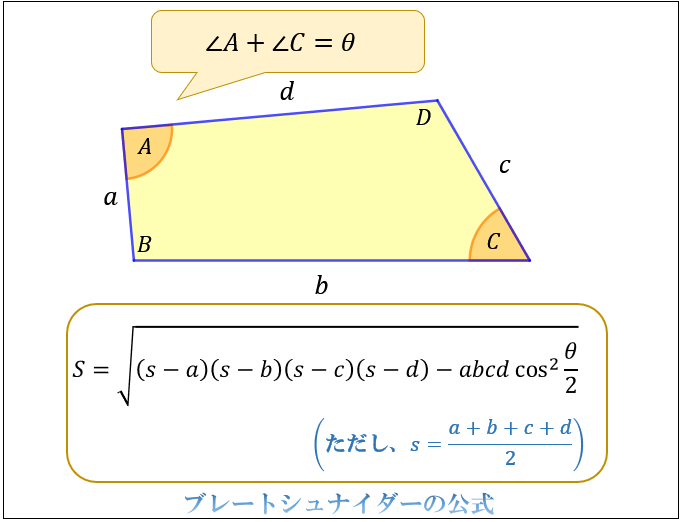



四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ



四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
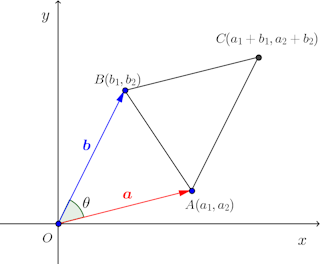
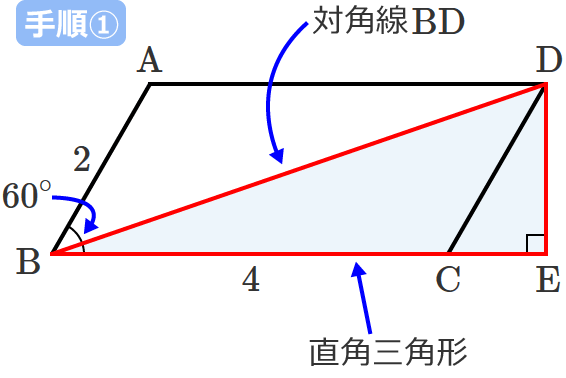
< 平面のベクトルと行列式> 原点を始点とする2つのベクトル a = ³ a1 a2 ´ ,b = ³ b1 b2 ´ に対して,原点O(0,0)と3点 A(a1,a2),B(b1,b2),C(a1 b1,a2 b2) をとると,四角形OACB は平行四辺形となる。 この平行四辺形の面積をS とする。aとbの位置関係が 図1のような 図をかくと、次のような状況です。 平行四辺形であれば、辺 AD と辺 BC は平行で長さが等しいため、ベクトルで書くと\ \overrightarrow{ \mathrm{ AD } }=\overrightarrow{ \mathrm{ BC } } \が成り立ちます。 D の座標を $(x,y)$ として、この式をベクトルの成分で書けば \begin{eqnarray}ア~ 1 平行四辺形の求め方を考える。 ・平行四辺形の面積の求め方を、具体物を切り 取り、変形する 小学校ではいろんな四角形の種類を習いますが、これらの定義や性質、面積の求め方など、様々なことを覚えないといけません。



三角形の面積 科学技術計算ツール




平行四辺形の面積の求め方 公式と計算例
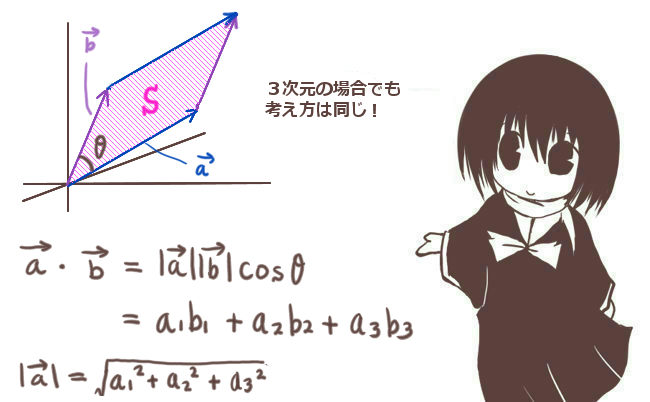
ベクトルの内積(スカラー積)と外積(ベクトル積)の成分表示 以上から、 s を動かし、各 s に対して t を動かすと考えれば、 P の存在範囲は、「平行四辺形 EBFI の周と内部」となることがわかります。 気が付かなかった方は、これから注意しましょう。2つのベクトル a a と b b から成る 平行四辺形の面積 S S は、 a a と b b の 外積 の長さ (ノルム) に等しい。 S= ∥a×b∥ S = ‖ a × b ‖ が成り立つ。 ここで、 θ θ はベクトル a a と b b の成す角であり、 0 ≤θ≤ π 0 ≤ θ ≤ π とする。 空間の平行四辺形の面積を求めるには下記のようにベクトルを使えば簡潔な公式で表せられます。 参考文献 基礎数学1 線型代数入門 齋藤正彦 (著) 東京大学出版会 しかし、成分表示にしようと思うと、とてつない数の項 (225項)が出てきて 手書きで計算



ベクトルの内積 スカラー積 と外積 ベクトル積 の成分表示




四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
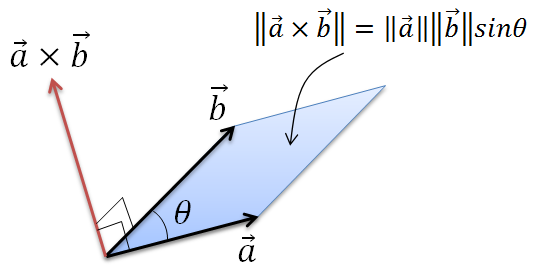
はベクトル , が なす平行四辺形の面積に等しい. 次 117 外積 上 1 ベクトルと図形 前 115 内積の幾何学的イメージ 平成年2月2日の作る三角形の 符号付き 面積 S は次のように求 めます. 点 P 1 を始点とした2 ベクトル を u 2 P 1 (2 x 1, 2 y 1) および ( ,) v 3 P 1 3 x 1 3 y 1 とするとき, 外積 uuv は2ベクトルの作る 平行四辺形の(符号付き)面積であるので,求めるべき三角形の 符号付き 面積外積を使うと,平行四辺形や三角形の面積,法線ベクトル,平面の方程式, 四面体の体積が楽に求められる場合がある。 外積の表し方 a とb の外積は,a b ´ あるいはb a ´ で与えられる。 外積の向き たとえば,a b ´ の向きは,
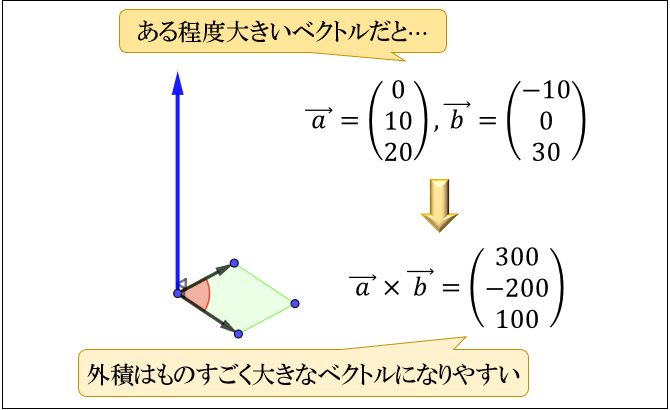



外積とは何か ベクトルの外積の定義 意味 大きさについて アタリマエ




外積の長さ 平行四辺形の面積 証明 理数アラカルト
1曲面の第1基本形式 これから3 次元ユークリッド空間における曲面を扱います. 曲面を表す方法はいくつかありますが,ここでは次の媒介変数表示の方法 を用います. U をR2 内の開領域.R2 内の点の座標を(u,v) で表します.U からR3 への1 対1 の写像をf とする.f の像S をユークリッド空間R3 内 平方四辺形を対角線で分けた $4$ つの三角形の面積は等しいから、平行四辺形の面積は、 $4\times \dfrac{3\sqrt{3}}{2} = 6\sqrt{3}$ だね! まとめ 平行四辺形の面積を対角線の長さと角度から求めるのに必要な特徴は、 平行四辺形の面積 まず, 2つのベクトル(ベクトルを横に書く悪習は辞めましょう) が張る平行四辺形の面積を考えよう 小学生でも習うこの公式 = (底辺) × (高さ) を思い出そう 底辺をとすると, これに対する高さは となる ここで, はとがなす角である すると, 面積は となる




ベクトル編 ベクトルで色々な図形を表現する 大学1年生もバッチリ分かる線形代数入門




ベクトル三重積と平行六面体及び四面体の体積 身勝手な主張




高校数学b ベクトルの外積 裏技 による法線ベクトル 空間の三角形の面積 平行六面体の体積 四面体の体積 受験の月




ベクトルを用いた三角形 平行四辺形の面積の公式と求め方 高校生向け受験応援メディア 受験のミカタ




勉強しよう数学 2重平行四辺形の面積の公式



ベクトルの平行条件 垂直条件とは 内積公式や証明 計算問題 受験辞典




平行四辺形の対角線の長さの求め方
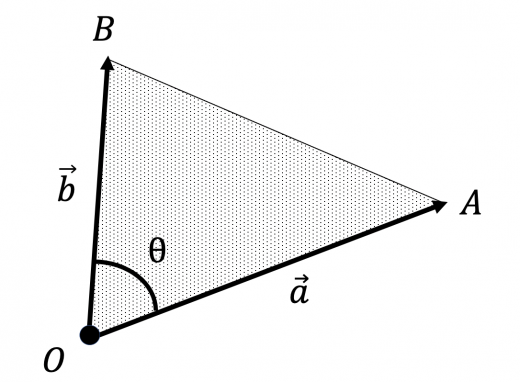



三角形の面積のベクトル 成分を用いた公式 高校数学の美しい物語



面積分




三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学
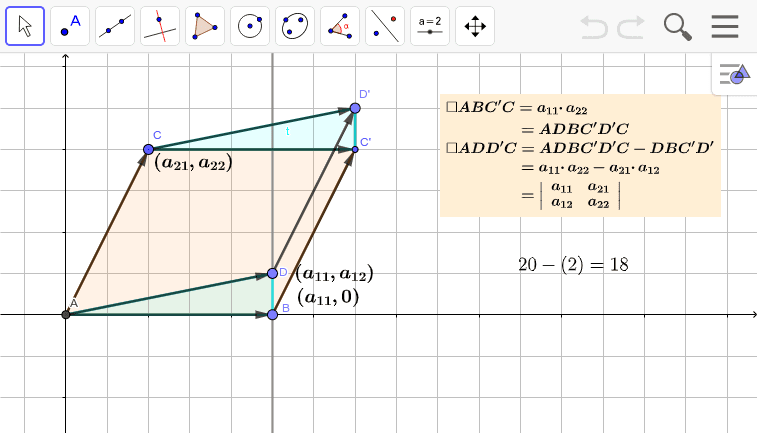



平行四辺形の面積と行列式 Geogebra




新訂版序文の人 大類昌俊 外出連続50日目 高校数学の参考書を読めば道具のように使われているのが分かるし 高校数学bで 平行四辺形の面積の公式 検定教科書では必須ではないが非常に便利 または大学数学でベクトル空間 空間ベクトル を学ぶ時の初等的な




高校数学 平行四辺形の面積の求め方 練習編 映像授業のtry It トライイット




勉強しよう数学 三角形の面積をベクトルで分解して計算する
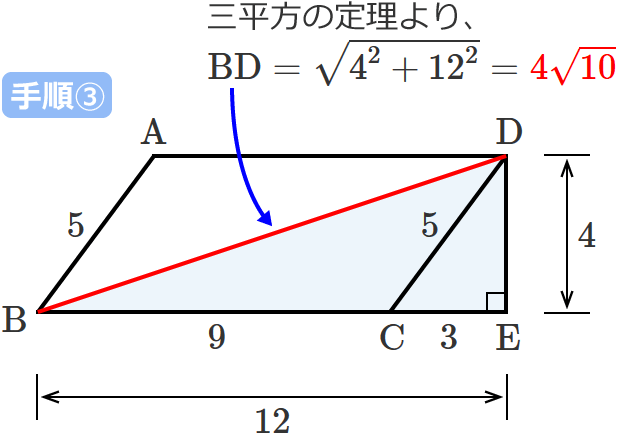



平行四辺形の対角線の長さの求め方



数学b ベクトルの範囲です 平行四辺形abcdの辺cdを3 1に内分する Yahoo 知恵袋




ベクトル方程式を超わかりやすく解説した 理系ラボ




ベクトル編 ベクトルで色々な図形を表現する 大学1年生もバッチリ分かる線形代数入門




ベクトルの外積と平行四辺形の面積 身勝手な主張
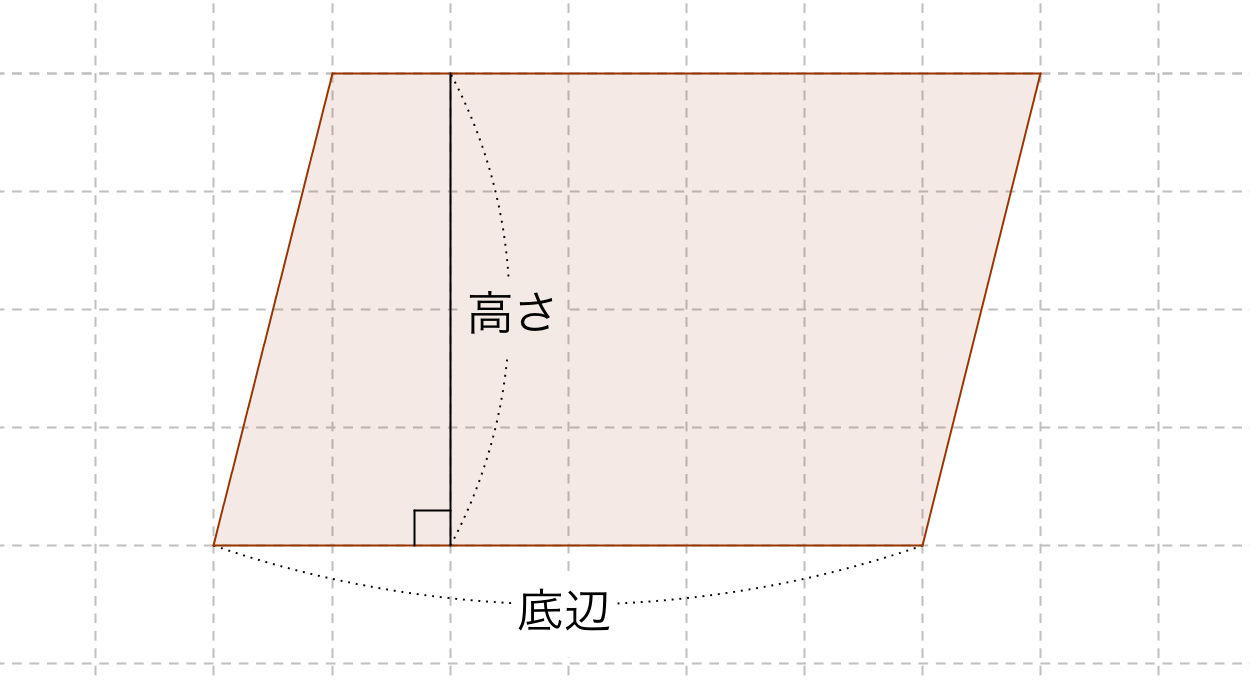



平行四辺形の面積の公式 算数の公式




勉強しよう数学 三角形の面積をベクトルで分解して計算する



平行性変形でのベクトルの小手技
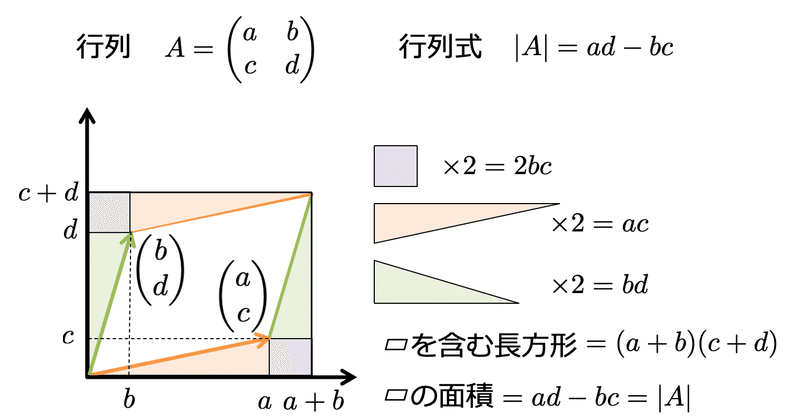



行列式 A Ad の幾何学的意味 Dr Kano Note



四角形の面積の求め方について質問です平行四辺形ではないいびつな四角形 Yahoo 知恵袋
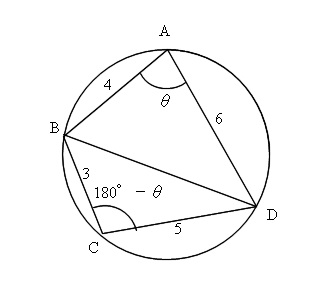



円に内接する四角形の面積の求め方と定理の使い方




外積の長さ 平行四辺形の面積 証明 理数アラカルト



3




平行四辺形の面積を求める公式 あまり知られていないかも 中学や高校の数学の計算問題




3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ



1




平行四辺形の面積 ベクトルでの公式 理数系無料オンライン学習 Kori
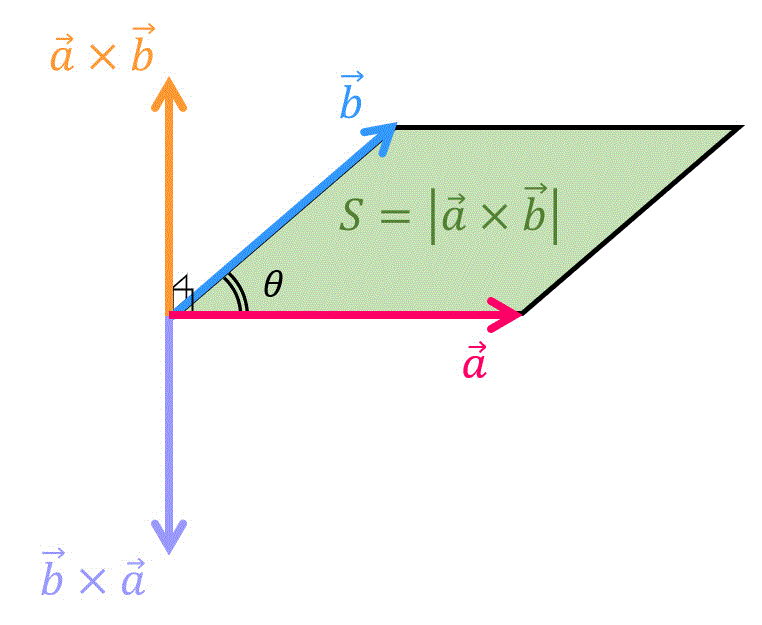



うさぎでもわかる線形代数 補充1 線形代数におけるベクトル 内積と外積 工業大学生ももやまのうさぎ塾
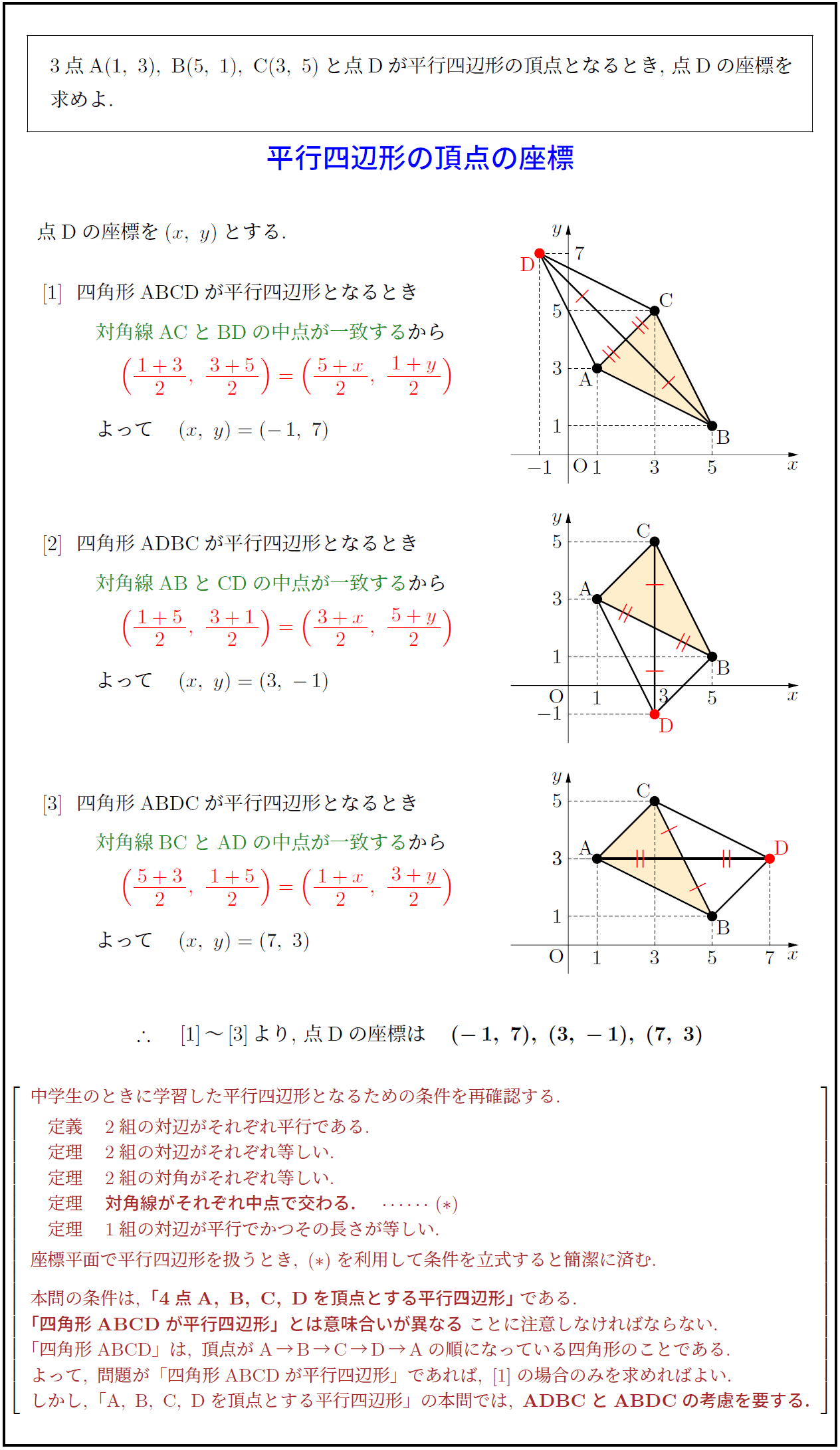



高校数学 平行四辺形の頂点の座標 受験の月




標準 平行四辺形とベクトルの演算 なかけんの数学ノート




高校数学 平行四辺形の面積の求め方 例題編 映像授業のtry It トライイット




相似 平行四辺形と面積比の問題を徹底解説 数スタ




ベクトルを用いた三角形 平行四辺形の面積の公式と求め方 高校生向け受験応援メディア 受験のミカタ



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典
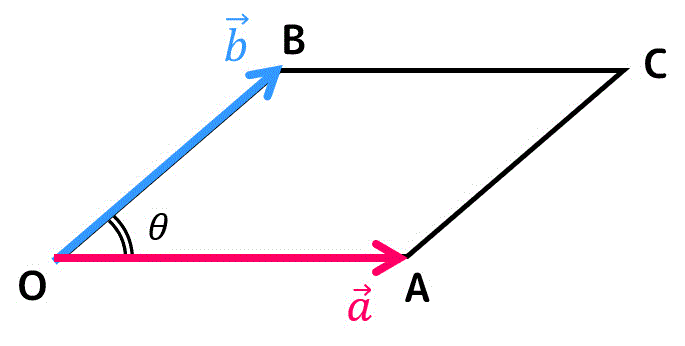



うさぎでもわかる線形代数 補充1 線形代数におけるベクトル 内積と外積 工業大学生ももやまのうさぎ塾




平行四辺形の面積 S Ad の証明2つ Youtube




倍横距法を用いて多角形の面積を求める方法




ベクトルを用いた三角形 平行四辺形の面積の公式と求め方 高校生向け受験応援メディア 受験のミカタ




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun




モデルの体積を計算する 試行錯誤




平行四辺形のベクトル 面積比の問題です 大学入試数学問題の解説 解答



ベクトル積の大きさは平行四辺形の面積 ベクトル解析 基礎からの数学入門



行列式 線型代数 数学教育




平行四辺形の面積の求め方 公式と計算例



Excelを使った数値計算ツールsuitexl



ねこ騙し数学
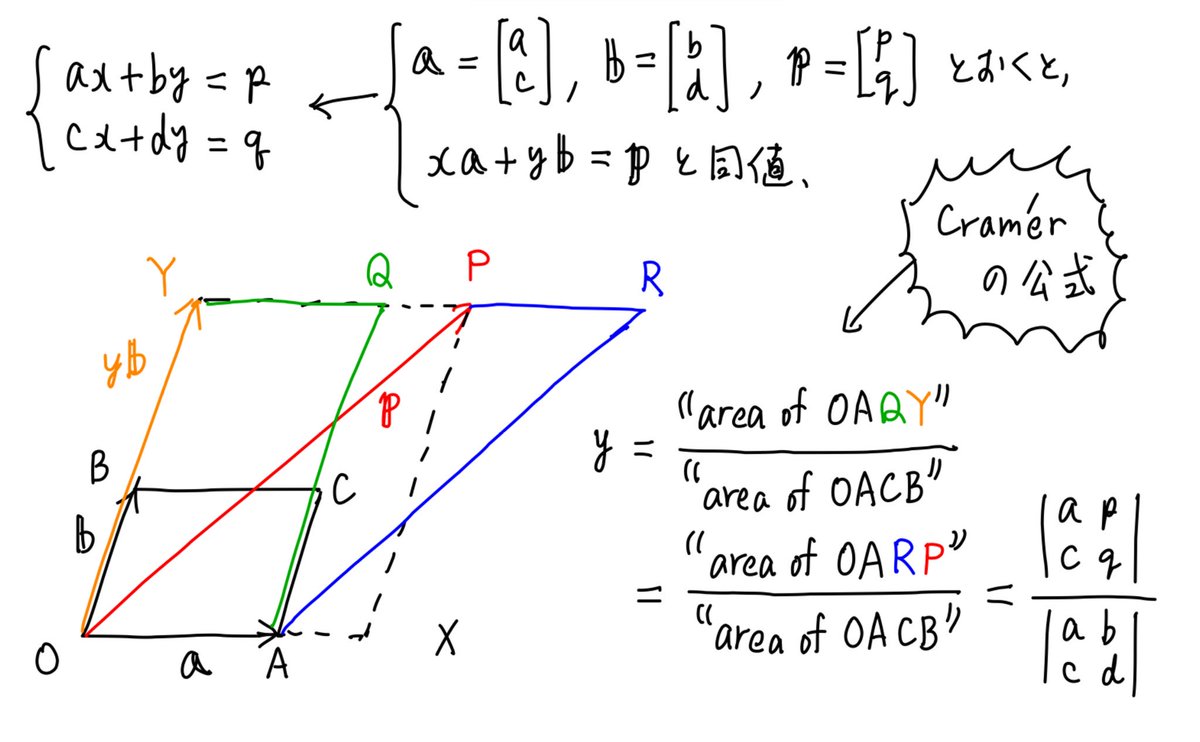



黒木玄 Gen Kuroki 数楽 行列式が体積 の 1倍 もしくは向き付けられた体積 だという事実も重要な数学的教養 高校でも問題練習のどこかで ベクトル A B と C D を2辺とする平行四辺形の面積が Ad になるという計算を含むものをやっているはず Ad




重心とは 三角形の重心の座標 位置ベクトルの求め方や公式の証明 面積比の問題を解説 数学 オイラー線 遊ぶ数学




ベクトルの外積と平行四辺形の面積 身勝手な主張




3 の平行四辺形の面積の求め方を教えてください 答えです 42 Clear




平行四辺形のベクトルの問題です 番の解き方を教えて下さい Clear




モデルの体積を計算する 試行錯誤



1
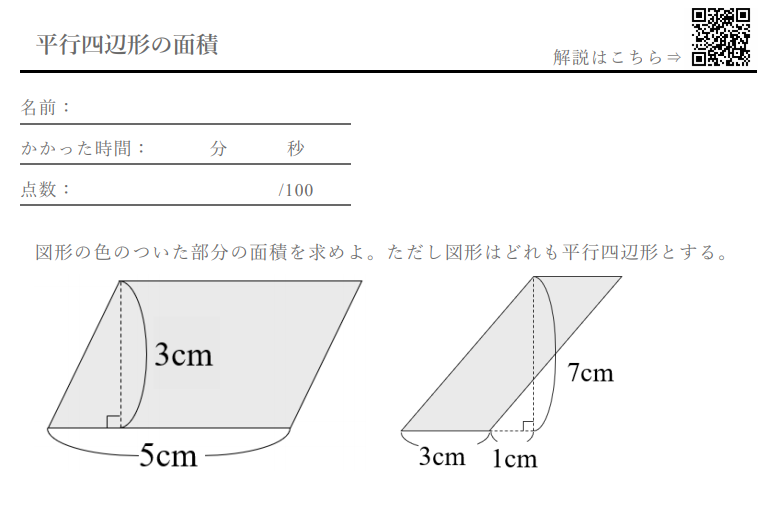



平行四辺形 の面積 計算ドリル 問題集 数学fun




三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学



3点からなる三角形の面積を求める イメージングソリューション



平面幾何におけるベクトル演算 内積と外積



3




外積を使って解く入試問題例 東大落ちの受験勉強法



平行四辺形の対角線の長さの求め方




高校数学b ベクトルの成分表示と平行四辺形 受験の月



ベクトルの外積をマスターしよう オンライン受講 東大に 完全 特化 東大合格 敬天塾



高校数学物理ベクトル平行四辺形a 1 2 3 B 3 2 1 の平行四辺 Yahoo 知恵袋



ベクトルの平行条件 垂直条件とは 内積公式や証明 計算問題 受験辞典



Fn 3次元空間における面の向きを調べる Flash テクニカルノート




ベクトルがつくる平行四辺形の面積 ベクトル13 数学検定1級はこれだけで合格できる




平行四辺形の面積の求め方 公式と計算例



Excelを使った数値計算ツールsuitexl




ベクトルを用いた三角形 平行四辺形の面積の公式と求め方 高校生向け受験応援メディア 受験のミカタ



数b 位置ベクトルの問題を教えてください 平行四辺形abcdの Yahoo 知恵袋



平行四辺形の面積 ベクトルでの公式 理数系無料オンライン学習 Kori




平行四辺形の対角線の長さの求め方




がわかりません アプローチの仕方も計算手順もさっぱり手詰まりです Clear




ベクトルを用いた三角形 平行四辺形の面積の公式と求め方 高校生向け受験応援メディア 受験のミカタ




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ




新訂版序文の人 大類昌俊 外出連続50日目 高校数学の参考書を読めば道具のように使われているのが分かるし 高校数学bで 平行四辺形の面積の公式 検定教科書では必須ではないが非常に便利 または大学数学でベクトル空間 空間ベクトル を学ぶ時の初等的な




ベクトル編 ベクトルで色々な図形を表現する 大学1年生もバッチリ分かる線形代数入門




標準 平行四辺形と座標 なかけんの数学ノート
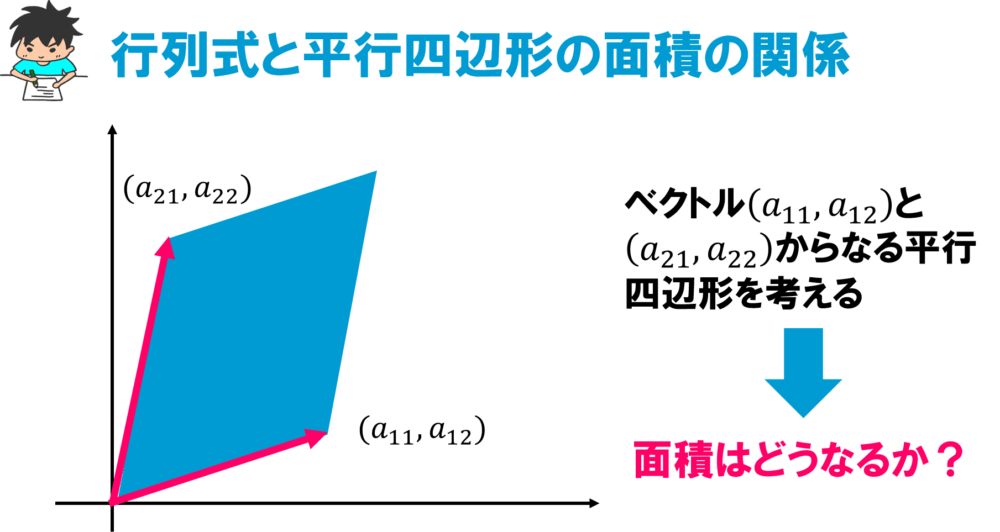



行列式の計算方法と図形的意味を解説してみる 線形代数を宇宙一わかりやすく解説してみるサイト




平行四辺形の面積を求めるある問題について 身勝手な主張




2次の正方行列式と平行四辺形の面積 機械学習に詳しくなりたいブログ




高校数学b 平行六面体と空間ベクトルの演算 受験の月
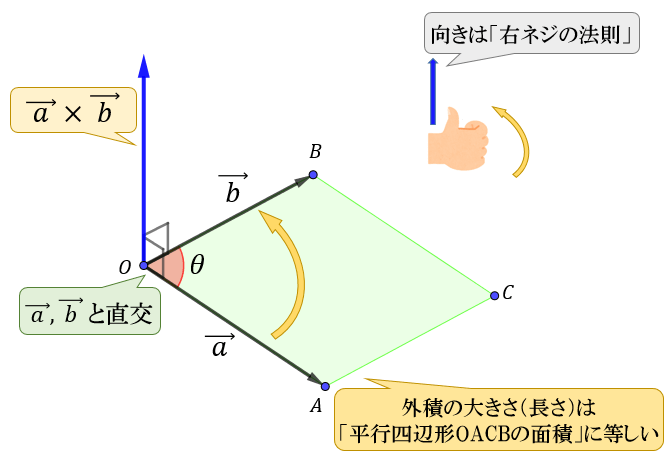



外積とは何か ベクトルの外積の定義 意味 大きさについて アタリマエ
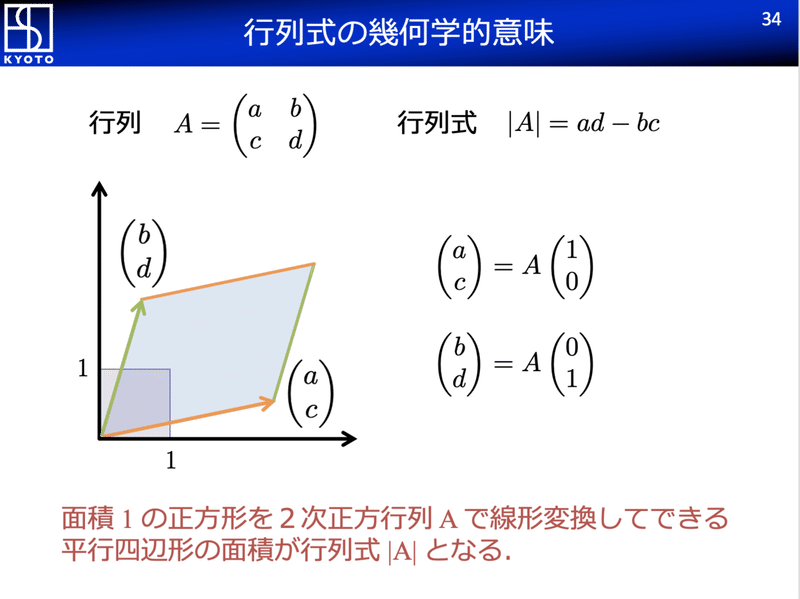



行列式 A Ad の幾何学的意味 Dr Kano Note



数学bの平行四辺形のベクトルの問題で 画像のof Odの答えの Yahoo 知恵袋
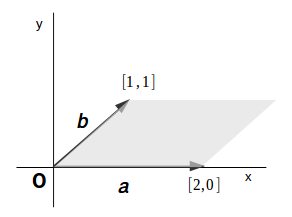



ベクトル積の大きさは平行四辺形の面積 ベクトル解析 基礎からの数学入門



0 件のコメント:
コメントを投稿