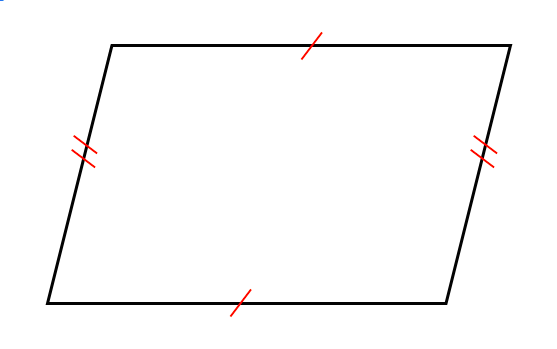
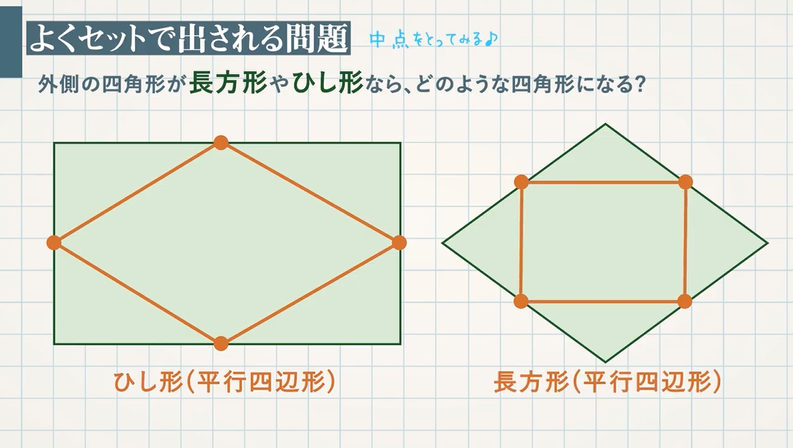
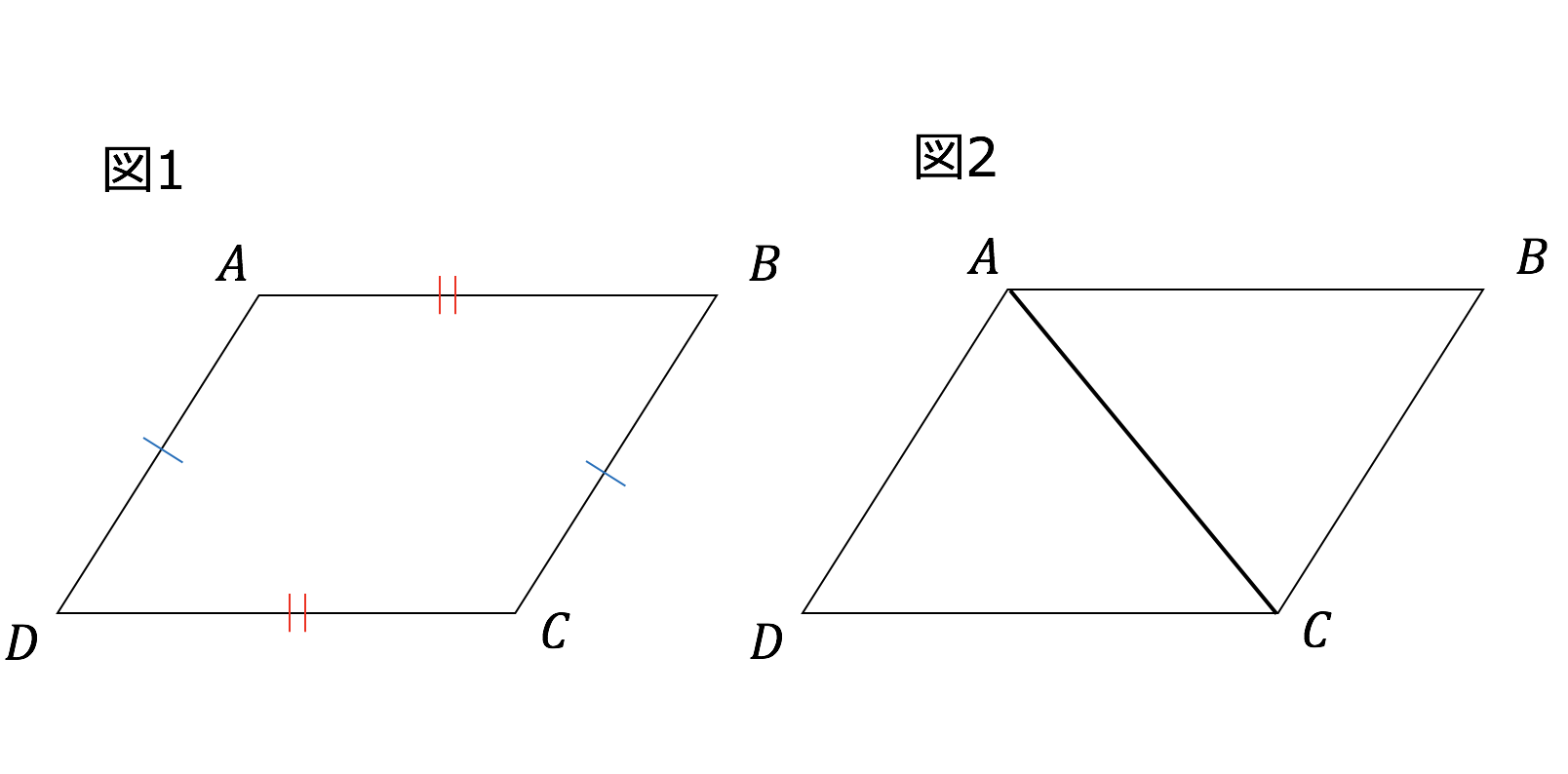
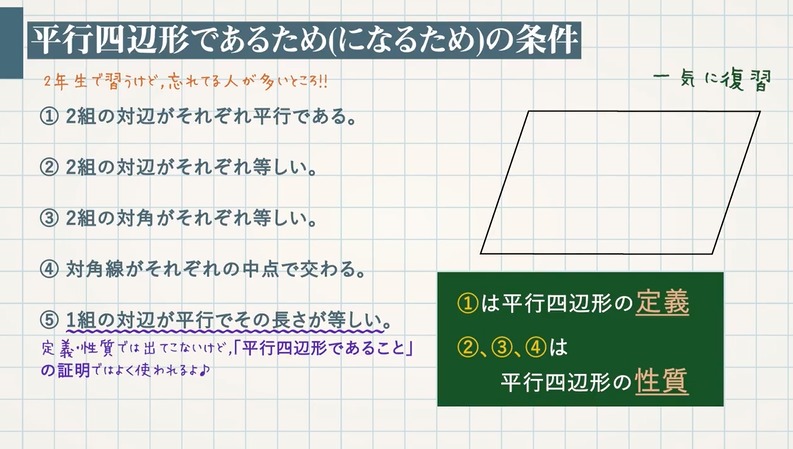
⑤ $\textcolor{blue}{1}$ 組の対辺が平行でその長さが等しい →定義・性質では出てこないけど、「平行四辺形であること」の証明ではよく使われます。 ①は平行四辺形の 定義 ②、③、④は平行四辺形の図形 定義・定理 まとめ 対頂角 𝟖は等しい 直線の角度 ° 平行線の 同位角 𝟖 は等しい 角形の内角の和 °×(𝒏− ) 平行線の 多角形の外角の和錯角 𝟔は等しい ° 同位角 が等しければ、2直線は平行 〇 合同な図形の対応する線分や角は等し定義から ( )=( ) ( )=( ) 2組の対角がそれぞれ等しいから 長方形abcdは平行四辺形である。 ひし形abcdにおいて 定義から 定理『二等辺三角形の頂角の二等分線は底辺を垂直に二等分する』を用いる。
平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典
平行四辺形の定義 定理
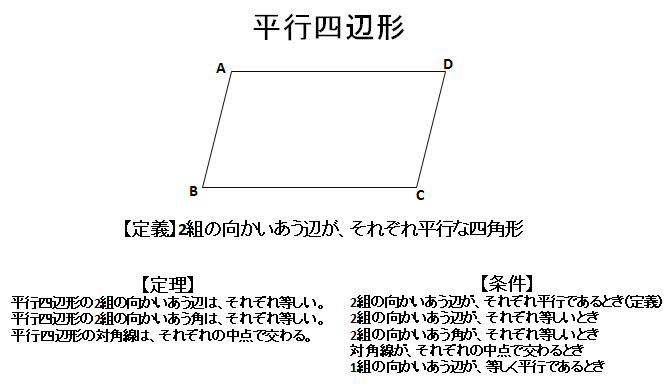
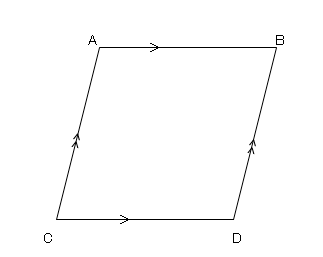
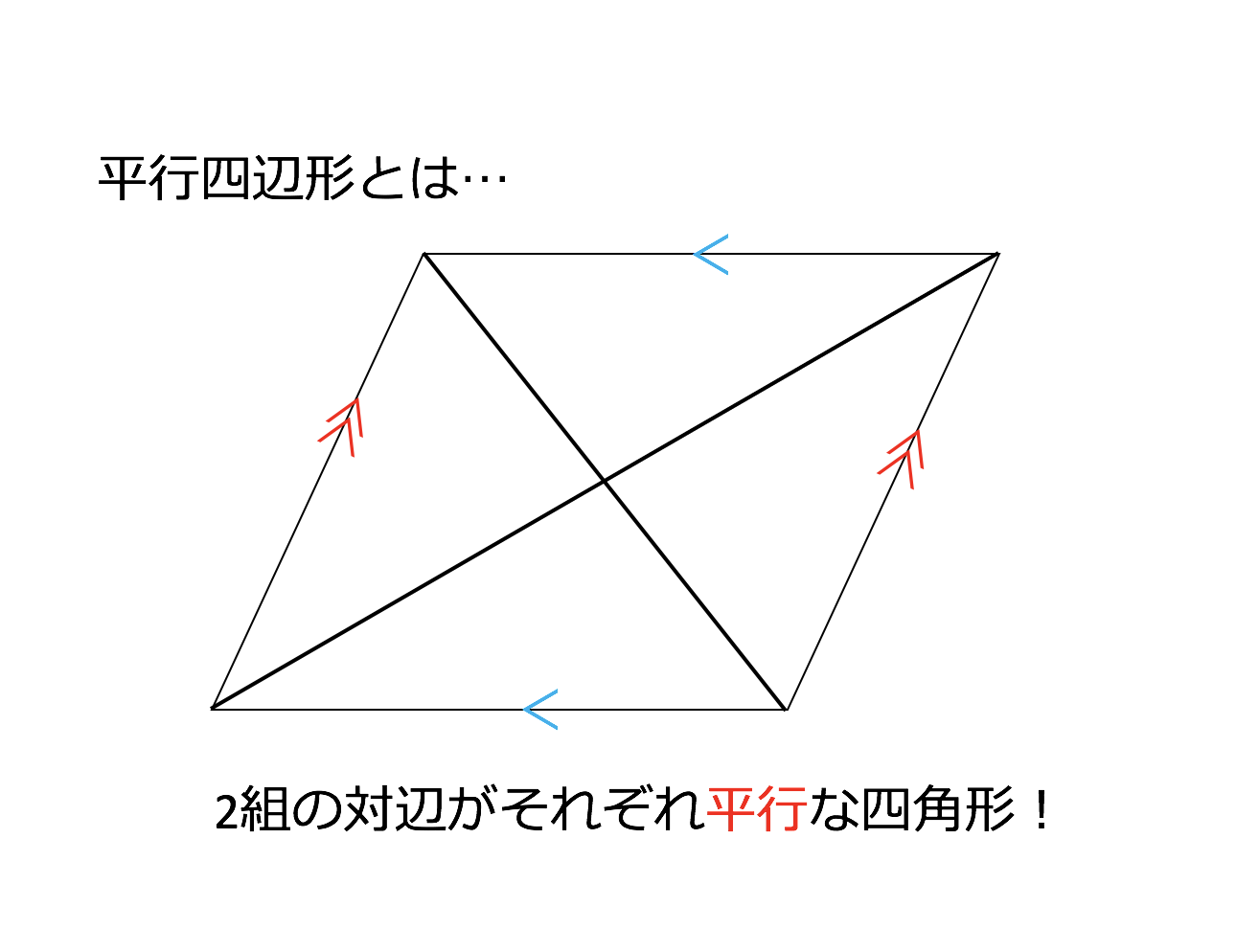
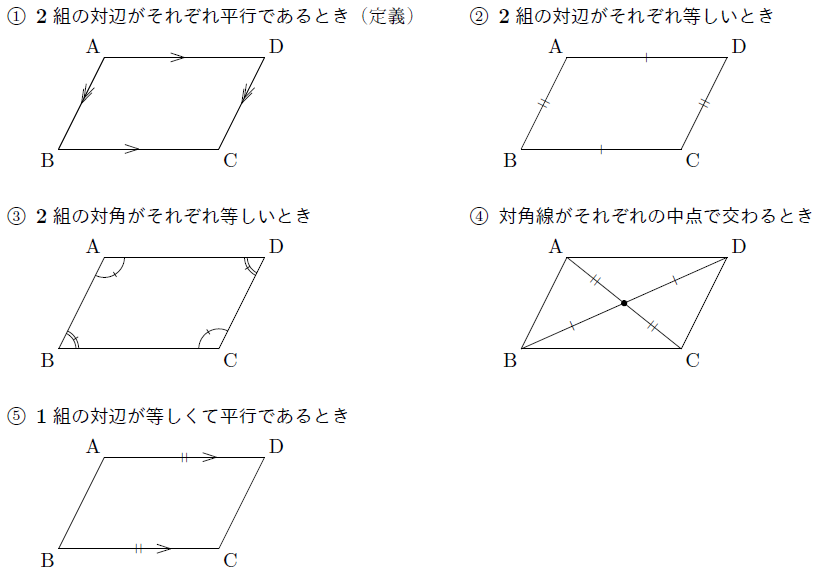
平行四辺形の定義 定理- 対辺・対角定義対辺:四角形の向かい合う辺対角:四角形の向かい合う角平行四辺形定義平行四辺形:2組の対辺がそれぞれ平行な四角形平行四辺形の定理定理平行四辺形の性質 2組の対辺はそれぞれ等しい 2組の対角はそれぞれ等しい 2つの対角定義 四角形abcdが平行四辺形とは ab∥dc,ad∥bc を満たす四角形である. 四角形で,向かい合う辺を 対辺 ,向かいあう角を 対角 といいます. 現時点では,平行四辺形では2組の対辺がそれぞれ平行であるしか使えません.



中学生ならおぼえたい 平行四辺形になる5つの条件 Qikeru 学びを楽しくわかりやすく
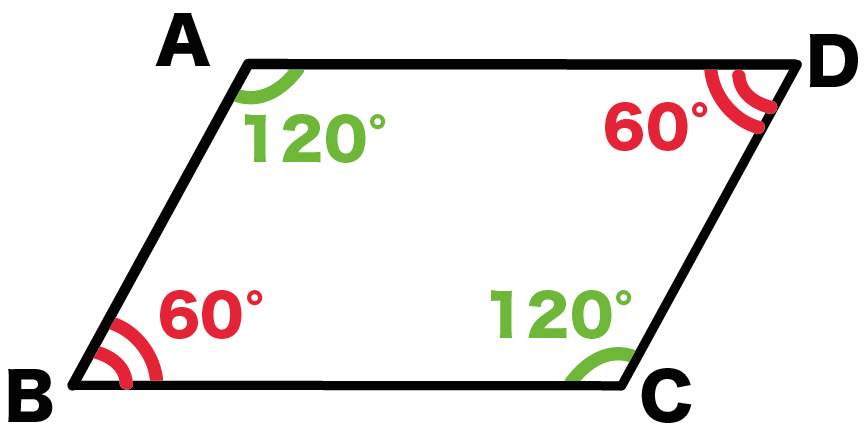
平行四辺形の定義と3つの定理の完成形(静止画) 動画 e1shi2mpg 3×240、 277MB 中学数学 ⇒ 図形の性質(中学2年) ⇒ いろいろな四角形 いろいろな四角形の定義 長方形,ひし形,正方形の定義をまとめています平行四辺形の定義と性質 定義 向かい合う2組の辺がそれぞれ平行な四角形 定理(性質) 2組の対辺がそれぞれ等しい 2組の対角がそれぞれ等しい 対角線がそれぞれの中点で交わる 定義は 「こういう四角形を平行四辺形としよう」 と決めたことなので平行四辺形の定義と性質を書きなさい。 定義: 性質(定理) ① ② ③ 2 右の図は、平行四辺形abcd の内部の点p を通り、辺ad、ab にそれぞれ平行な直線ef、gh
間違いではありませんが、この図は平行四辺形の一例を示しただけです。 平行四辺形の定義は「 2組の向かい合う辺が、それぞれ平行な四角形 」です。 ですから 正方形も長方形も平行四辺形の仲間であると言えます。平行四辺形の定義は、「\(\boldsymbol{2}\) 組の向かい合う辺が平行な四角形を平行四辺形という 」になります。また、平行四辺形になるためには、定義を含めて \(\boldsymbol{5}\) つの条件 があります。 中学全学年 正方形、長方形、ひし形、平行四辺形の定義と定理をまとめてあります。 定義 定理 図形 このノートが参考になったら、著者をフォローをしませんか? 気軽に新しいノートをチェックすることができます!
平行四辺形 (へいこうしへんけい、英 parallelogram)とは、2組の対辺がそれぞれ 平行 である 四角形 のことである。 平行四辺形の条件 ある平面図形が平行四辺形であるための条件には、次の \(5\) つがあります。 このうちどれか \(1\) つでも条件を満たせば、その図形は平行四辺形と言えます。 条件①2 組の向かい合う辺が平行である これは平行四辺形の定義と同じ平行四辺形とひし形の違いってなに??←今回の記事 平行四辺形の角度、辺の長さを求める問題を解説! 平行四辺形の中から面積の等しい三角形を見つける問題を徹底解説! 等積変形三角形の面積問題と作図のやり方は?証明問題も紹介!



平行四辺形とは 1分でわかる意味 定義 角度 面積 長方形と正方形との関係



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典
数学・算数 平行四辺形の定義と性質について 現在某学習塾で塾講師としてアルバイトをしている大学生です。 先日中学2年生の生徒に平行四辺形の定義と性質について教えていたのですが、その生徒からとある 質問No9101 ; 4つの角がすべて等しい四角形 が「長方形の定義」っておぼえておこう。 長方形は平行四辺形の仲間なの?? 1つだけおさえておきたいことがある。 それは、 長方形は平行四辺形の1種 ってことさ。 つまり、 長方形は平行四辺形である といえちゃうんだ。平行四辺形の定義 ①定義 2組の対辺がそれぞれ平行である。 ②定理 2組の対辺がそれぞれ等しい。 ③定理 2組の対角がそれぞれ等しい。




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典
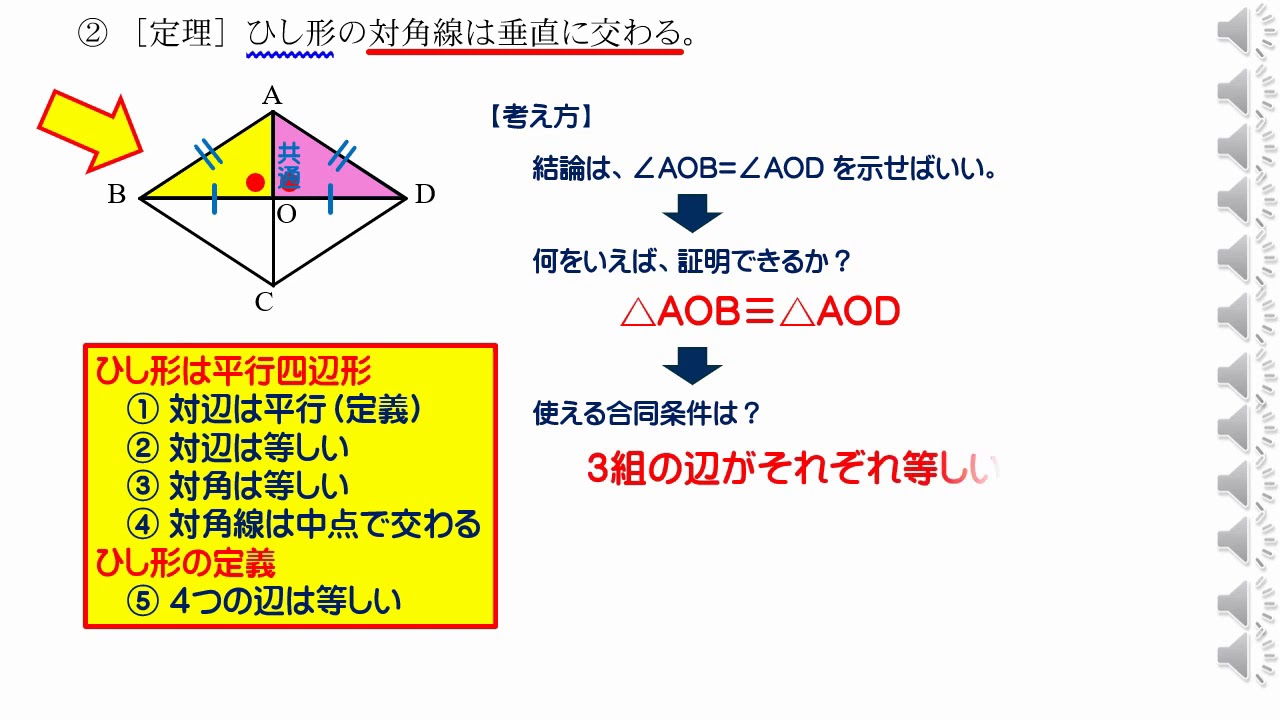
定義 4つの辺の長さが全て等しい四角形をひし形という。 定理 ひし形の2組の向かい合う辺はそれぞれ平行で長さが等しい。 定理 ひし形の2組の向かい合う角の大きさはそれぞれ等しい。 定理 ひし形の対角線はそれぞれ中点で垂直に交わる。 定理1平行四辺形とは? 平行四辺形は、向かい合う2組の辺が平行な四角形と定義されます。 向かい合う辺のことを 対辺 ,向かい合う角のことを対角と呼びます。 2ポイント ただし,「平行四辺形=2組の対辺が平行」と覚えるだけでは,中学数学の問題は解けません。平行四辺形の定義は 「2組の対辺が、それぞれ平行である四角形」 平行四辺形の定理 1 平行四辺形の2組の対辺は、 それぞれ等しい。 2 平行四辺形の2組の対角は、 それぞれ等しい。 3 平行四辺形の対角線は、 それぞれの中点で交わる。 1 2組の対辺が
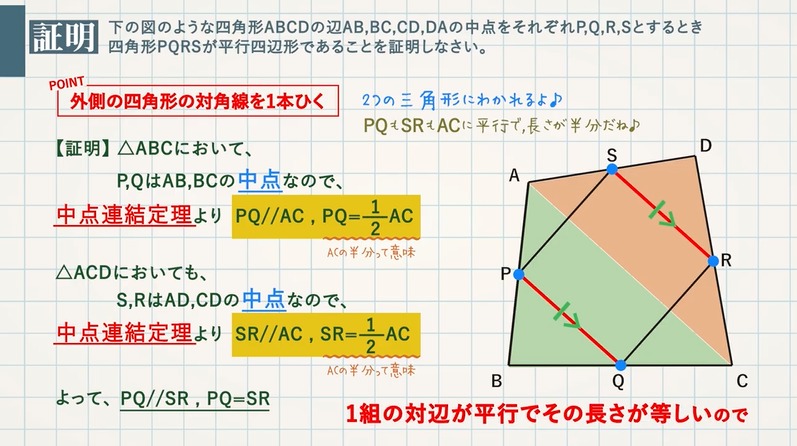



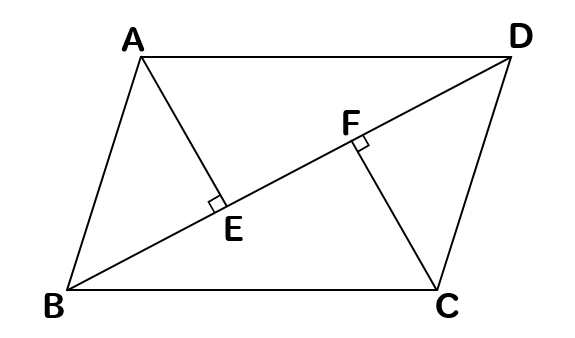
中点連結定理を使った平行四辺形であることの証明 教遊者




スプリックス 平行四辺形の定義と性質 1 Youtube
「定義」は用語の意味を明確にしたもの。つまり、 「2組の対辺がそれぞれ平行な四角形を平行四辺形と呼ぶ」 ということです。 「定理」は、すでに正しいということが証明された性質のこと。 いちいち証明しなくても使っていいよ、ということです。 平行四辺形の定義と定理について ① 二組の対辺がそれぞれ平行 ② 〃 等しい ③二組の対角がそれぞれ等しい ④対角線がそれぞれの中点で交わる ⑤一組の対辺が平行でその長さが等しい ②~⑤は①を基に証明できますが、②を定義とし①を証明することは可能なのでしょうか?定義 定義 定理(性質) 定義 定義 定理(性質) 定義 定理(性質) 定義 定理(性質) 正方形 ・ ・ ひし形 ・ ・ ・ 平行四辺形に なる条件 平行四辺形 ・ ・ 長方形 ・ 定理(性質) ・ ・ ・ ・ ・ ・ 直角三角形の合同条件 ・ ・ ・ ・ 定理(性質) 二等辺



中2数学 平行四辺形の性質と証明の要点まとめノート 中学生勉強サイトあかね先生



特別な平行四辺形 Youtube
と書く事もできるので平行四辺形の法則とも言われる。 内積空間における中線定理 中線定理は内積を有するベクトル空間(内積空間、計量ベクトル空間)の一般的性質としてとらえることができる。内積空間v に対し、内積によって定義されたノルム そして、この定義と「平行線の同位角は等しい」という公理から 三角形の内角の和は180度ということが証明できます。 このように 定義や公理から証明できるものを定理 と言います。 定理から定理を証明することもできます。簡単に説明すると、 「定義」 :こういうものを平行四辺形と呼ぼう! 「性質」 :平行四辺形と呼ばれるものには 共通してこんなことが言えるね! 「定理」 :性質の中で特に大切なこと! だから証明はいらないよ! こんな感じです。 例えば



平行四辺形 1 ネット塾




平行四辺形 中学数学で遊ぶ 身勝手な主張
台形: 向かい合う1組の辺が平行な四角形 注意点として、 "長方形" や "ひし形" も向かい合う辺は平行なので 『平行四辺形の定義』 に当てはまりますし、 "正方形" は 『長方形・ひし形の定義』 にも当てこんにちは、ウチダです。 今日は、中学 $2$ 年生の内容である 「平行四辺形になるための $5$ つの条件」 について、平行四辺形の定義から性質を証明し、そのあとで性質と条件が具体的にどう違うのかを詳しく見ていきましょう。 平行四辺形の定義とは まず、「平行四辺形とは何か」口で説明平行四辺形の定義 } 2組の対辺がそれぞれ平行であ る四角形を平行四辺形という 平行四辺形の定理 ①平行四辺形の2組の対辺は それぞれ等しい ②平行四辺形の2組の対角は それぞれ等しい ③平行四辺形の対角線は それぞれの中点で交わる



中学数学 平行四辺形の証明問題を徹底解説 数スタ




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学




Left 3 Ableft D Abdc Ad Descubre Como Resolverlo En Qanda



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典



平行四辺形の定義




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ




平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室



平行四辺形について知ろう 苦手な数学を簡単に




平行四辺形の定義と性質 証明問題の解き方 数学fun



高校入試 英語 数学 学習 三角形と四角形 平行四辺形



中点連結定理を使った平行四辺形であることの証明 教遊者




山と数学 そして英語 平行四辺形の定義や定理と 数学における暗記について



テボールの定理 雑学のソムリエ



1




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学



平行四辺形で知っておくべきこと 苦手な数学を簡単に




中学校数学 証明のコツ 年01月




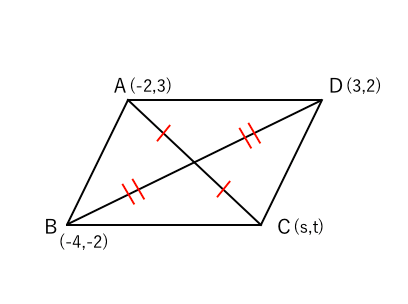
関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ
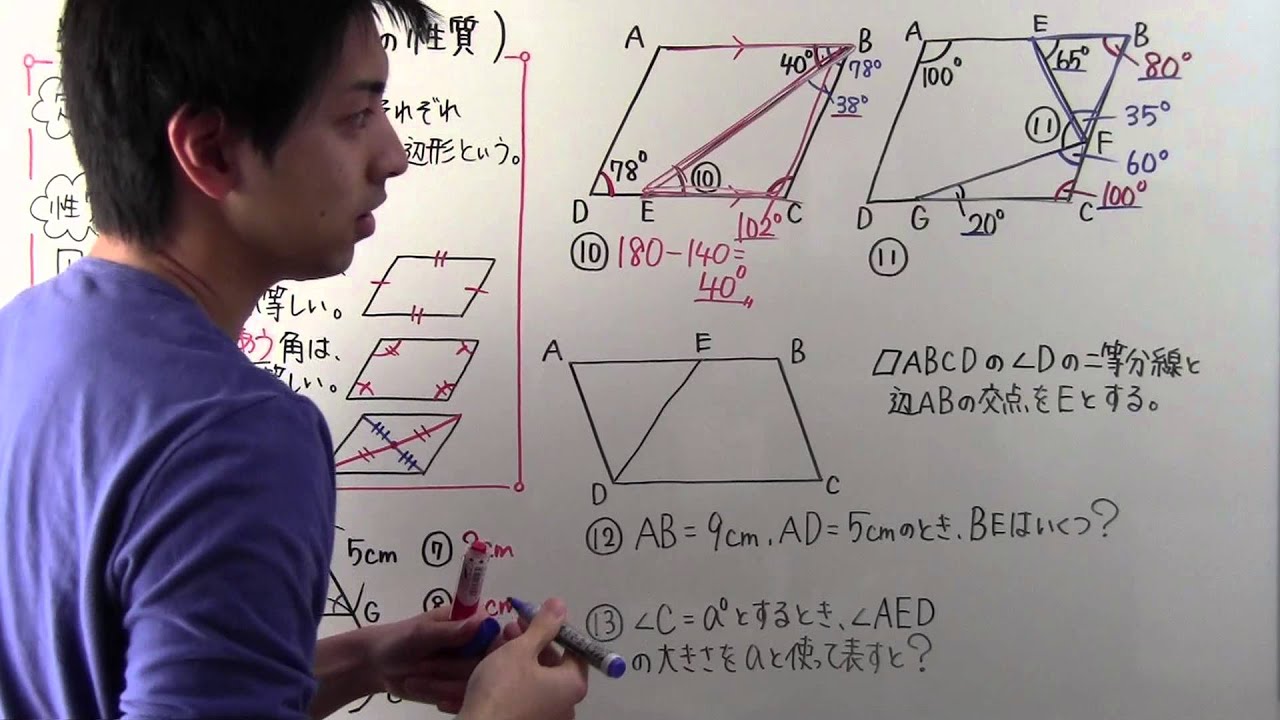



数学 中2 73 平行四辺形の性質 Youtube




壮大 平行 の 定義
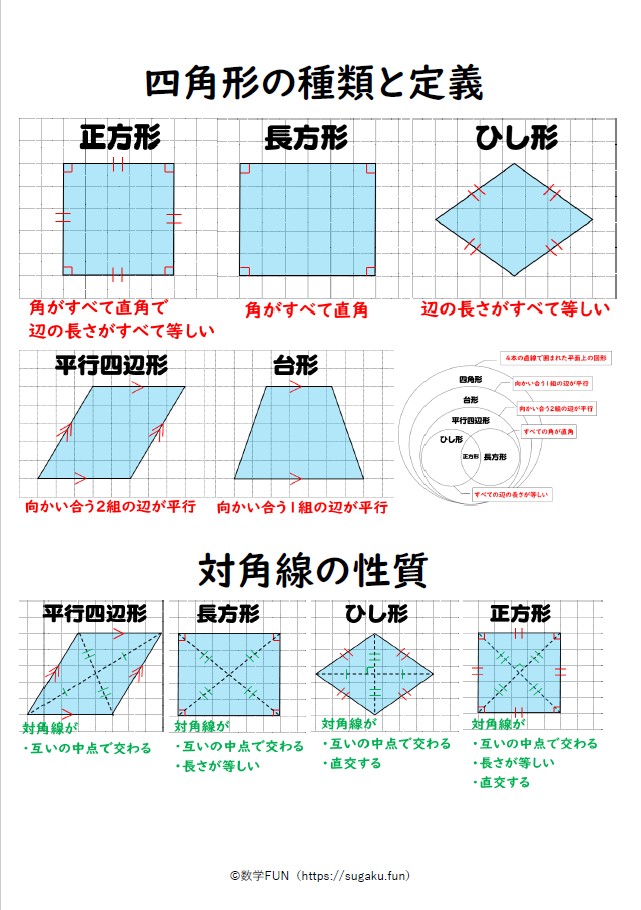



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




中学校数学 証明のコツ 年01月



平行四辺形とは 1分でわかる意味 定義 角度 面積 長方形と正方形との関係




平行四辺形の辺や角を求める Youtube
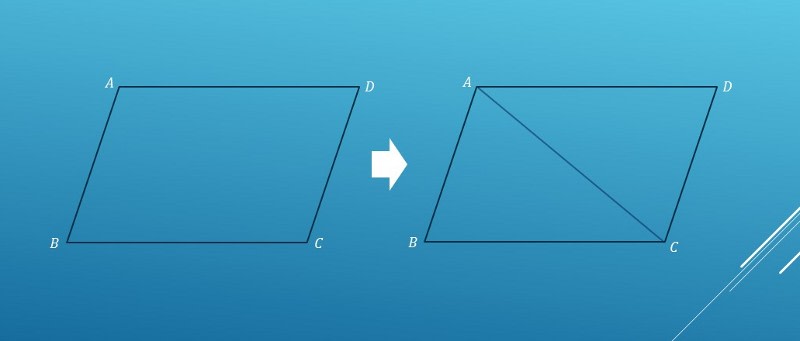



高校入試と 平行四辺形の定義と定理について 中学生 受験対応 英語 数学 学習講座
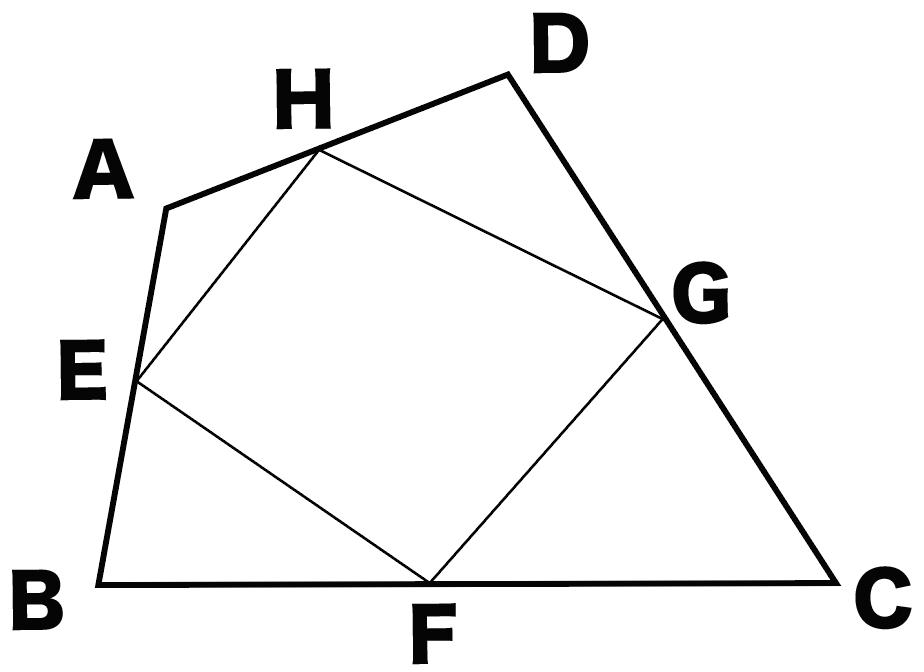



中点連結定理 平行四辺形の証明問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく




平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を押さえよう 遊ぶ数学




これ 問題の中に1つも平行ってワードがないのに どうして中点連結定理になるのか そし Clear




3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学




Math 平行四辺形 平行四辺形になることの証明 働きアリ
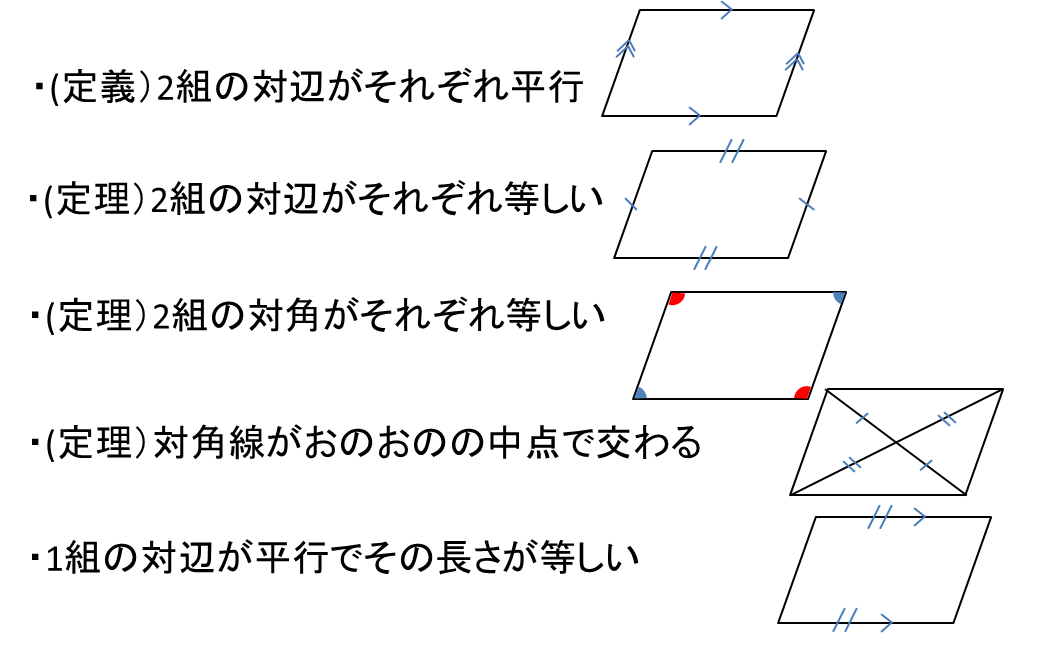



140字で高校受験 数学 平行四辺形の定義 性質 なるための条件 言葉だけでなく図で覚える T Co Amwmvf58n7




中学数学 特別な平行四辺形について Clear




定義と定理 12月 年 光が丘中学校 ブログ 光が丘中学校



1




数学の問題の解き方を教えてください Clear
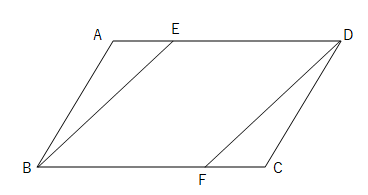



中2数学 平行四辺形の証明のポイントと練習問題 Examee




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット



平行四辺形に関する定理 雑学のソムリエ




平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を押さえよう 遊ぶ数学




中学校数学 証明のコツ 年01月




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ




中学生ならおぼえたい 平行四辺形になる5つの条件 Qikeru 学びを楽しくわかりやすく
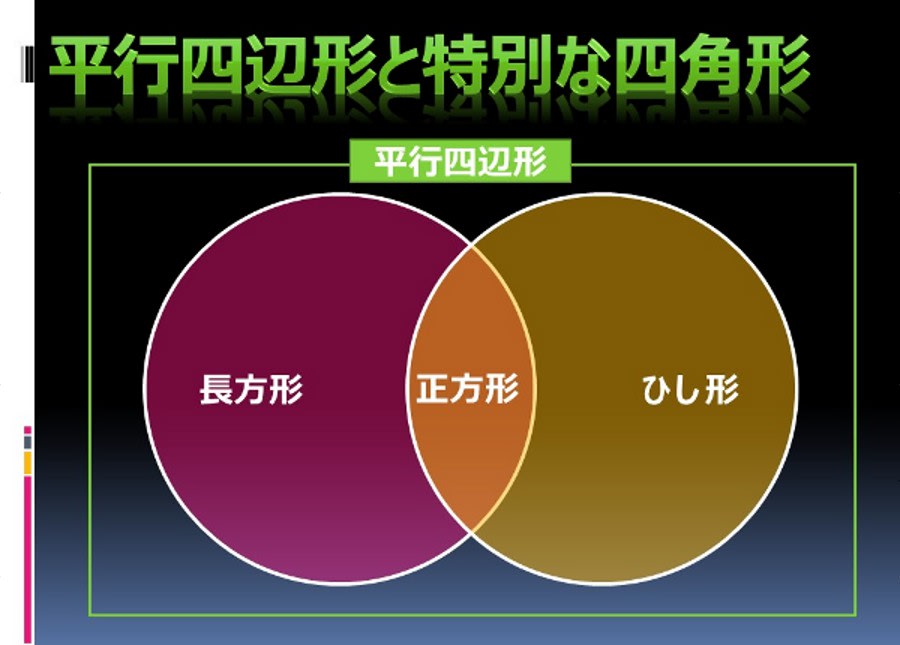



高校入試と 平行四辺形の定義と定理について 中学生 受験対応 英語 数学 学習講座




等脚台形の定義と性質 中学校数学の範囲内で考える 身勝手な主張



中2数学 平行四辺形の3つの性質 Qikeru 学びを楽しくわかりやすく



中点連結定理とは 証明 定理の逆や応用 問題の解き方 受験辞典




平行四辺形の定義と性質 証明問題の解き方 数学fun




平行四辺形の対角線の長さの求め方




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ



3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ



Http Www Edu City Misato Lg Jp Secure 0526teigi Teiri Kotae Pdf



3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ




中学生ならおぼえたい 平行四辺形になる5つの条件 Qikeru 学びを楽しくわかりやすく



中点連結定理を使った平行四辺形であることの証明 教遊者



1




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ




平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は4つ 中学や高校の数学の計算問題




平行四辺形 現役塾講師のわかりやすい中学数学の解き方



平面図形の基礎



平行四辺形について知ろう 苦手な数学を簡単に




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット




平行四辺形である事を証明する上で大切な事 またはポイントなどはありますか Clear




平行四辺形 中学数学で遊ぶ 身勝手な主張




中2 授業ノート 平行四辺形の性質 中学生 数学のノート Clear
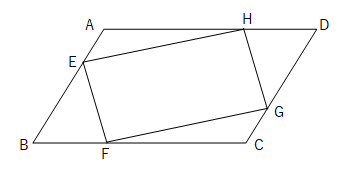



中2数学 平行四辺形の証明のポイントと練習問題 Examee




台形と平行四辺形を平行な辺の組の数で分類することは 原理的に不可能である 小学校4年生の算数 身勝手な主張



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ



高校入試 英語 数学 学習 三角形と四角形 平行四辺形
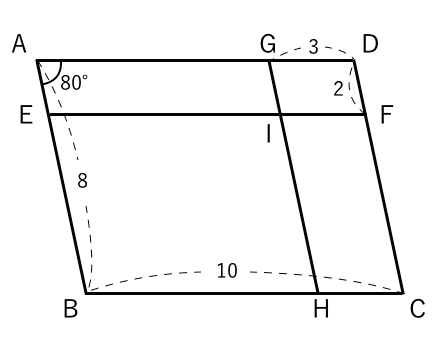



三角形の合同 平行四辺形 苦手な数学を簡単に




壮大 平行 の 定義




高校数学b ベクトルの成分表示と平行四辺形 受験の月




中点連結定理を使った平行四辺形であることの証明 教遊者




平行四辺形 Wikipedia




3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ




中点連結定理とは 逆の証明や平行四辺形の問題もわかりやすく解説 遊ぶ数学



1



平面図形の基礎




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット
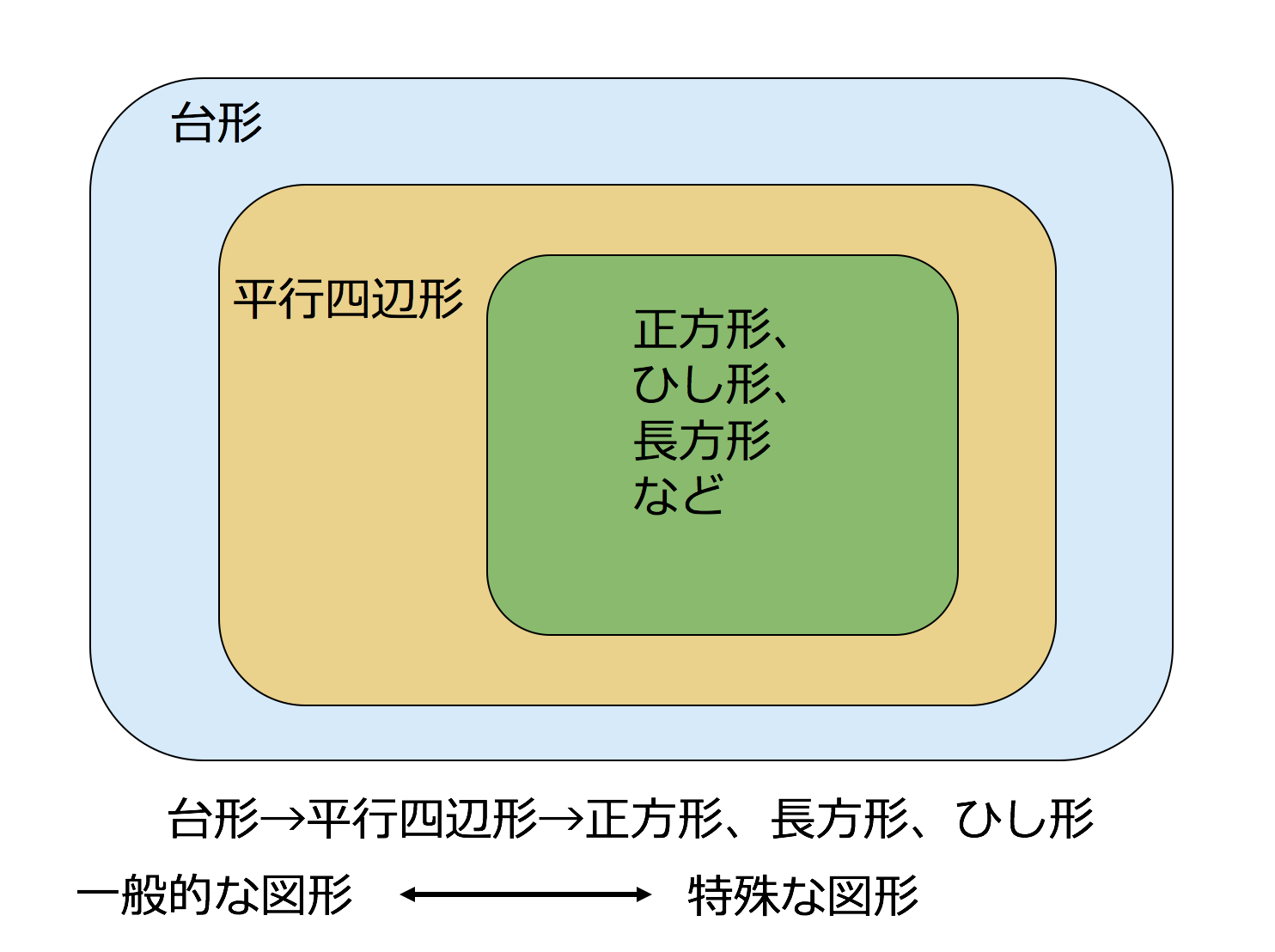



3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ



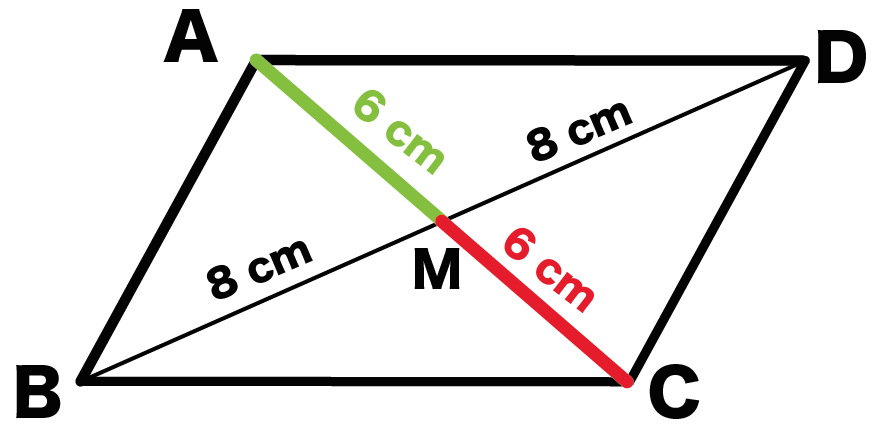
平行四辺形になるための条件 まなびの学園



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット




平行四辺形になることの証明 Youtube




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット




数学も英語も強くなる 意外な数学英語 Unexpected Math English Rhomboid
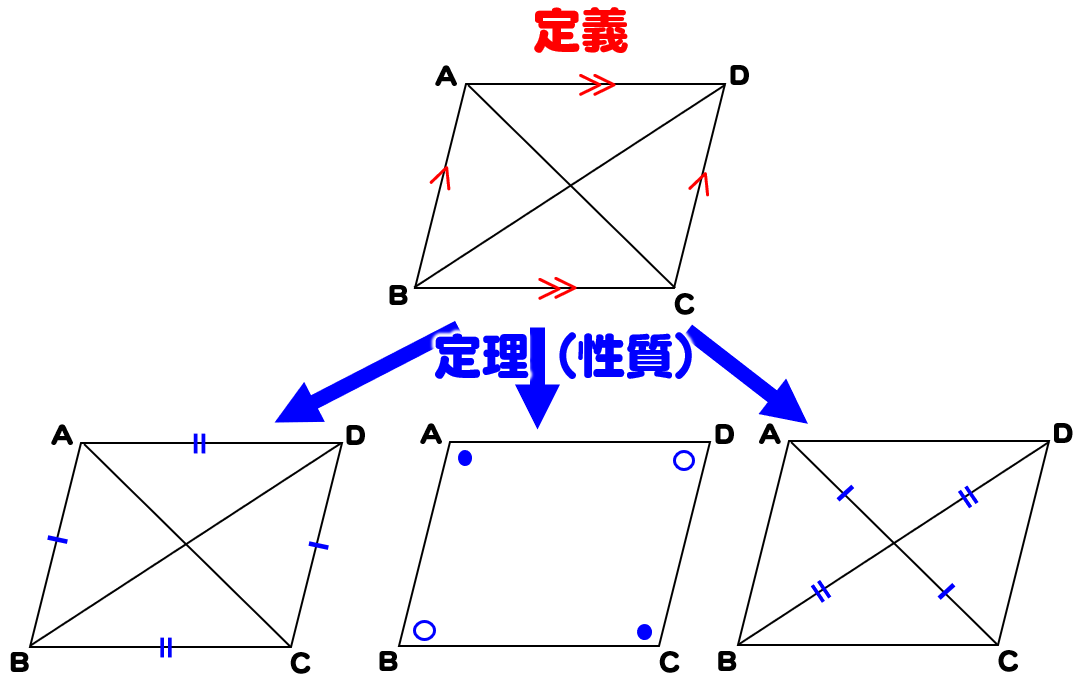



平行四辺形の定義と性質 証明問題の解き方 数学fun



0 件のコメント:
コメントを投稿