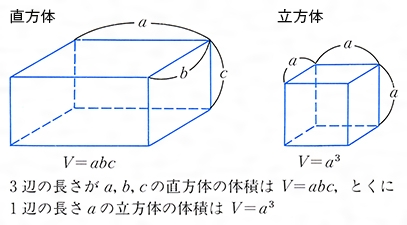
三角柱の高さをかけるっ! さっき計算した「底面積」に「三角柱の高さ」をかけてみよう! なぜなら、 底面積×高さ を計算すると立体の体積を求めることができるからね。 例題でいうと、 Step1で計算した底面積は10 cm^2、三角柱の高さは10 cmだから、 三角柱ABCDEFの体積は、立方体の体積 立方体の体積 立方体の辺の長さから体積と表面積を計算します。 立方体の辺の長さ 立方体の辺の長さ 立方体の体積から辺の長さと表面積を計算します。 直方体の体積 直方体の体積 直方体の三辺の長さから体積と表面積を計算します。無料ダウンロード・印刷できる、立体の体積を求める問題プリント です。 直方体と立方体を組み合わせた立体の体積を求める問題を繰り返し練習できます。 当ページのプリントの解答では、解答式を一例としてのせています。 どのように式を組み立てて立体の体積を求めるかは様々な考え方があります。 学校のテスト等では、お使いの教科書や教わっている先生
小5 直方体の体積 複雑な立体を求める 日本語版 Youtube
体積の求め方 立方体 リットル
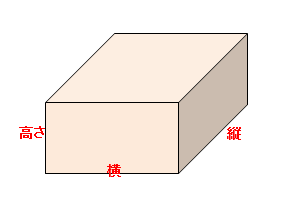
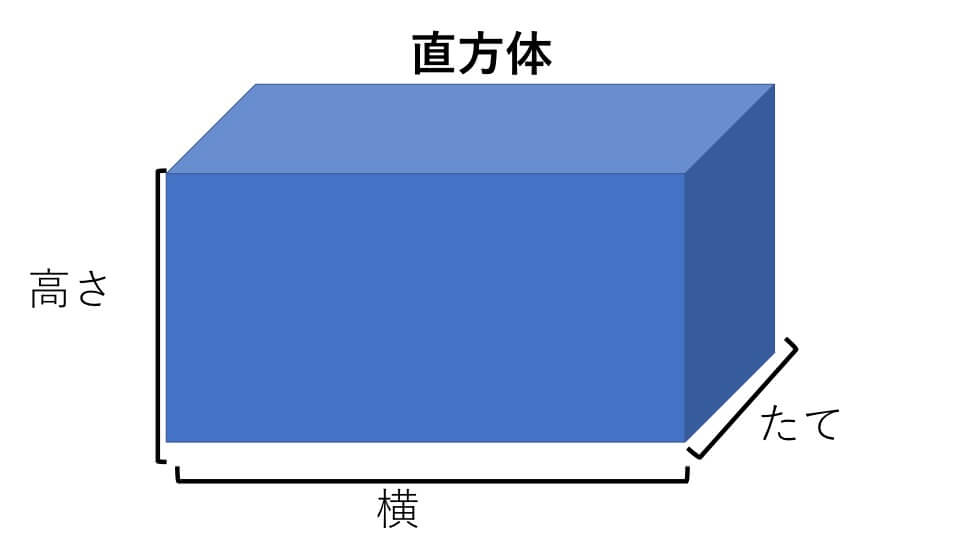
体積の求め方 立方体 リットル-直方体と立方体の体積、体積の求め方のくふう、高さと体積の関係、いろいろな体積の単位 小学5年生 講師 葉一(はいち)体積の求め方 そもそも、体積の求め方は、どうやるのか? 小学校で体積を求める方法を習う立体は、立方体と直方体とそれらを組み合わせた立体です。 それぞれの体積の求め方を調べてみると、 直方体:縦×横×高さ 立方体:1辺×1辺×1辺 と書いています。




中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー
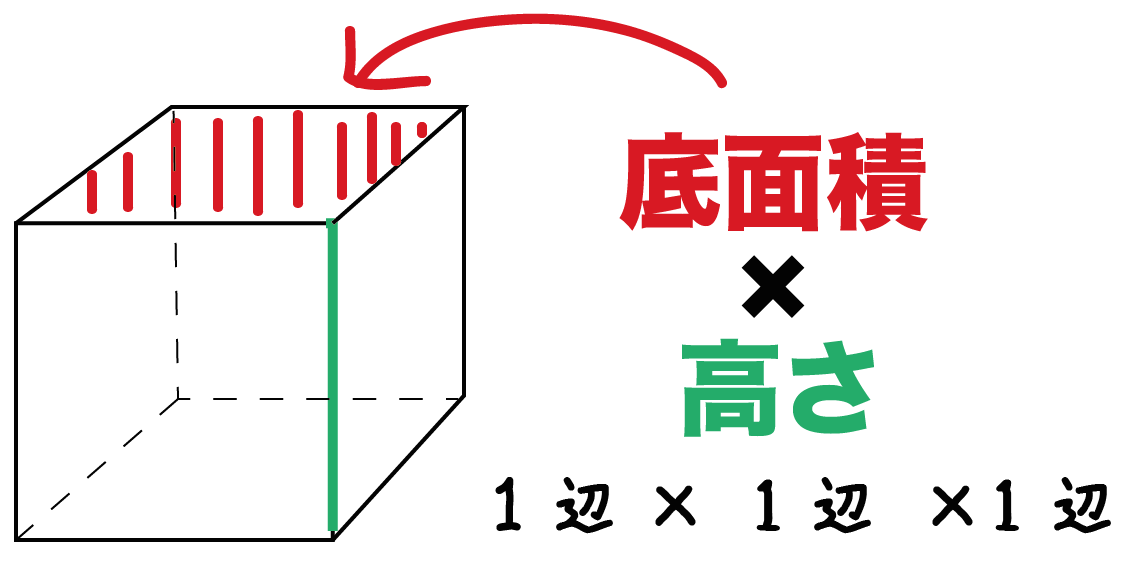
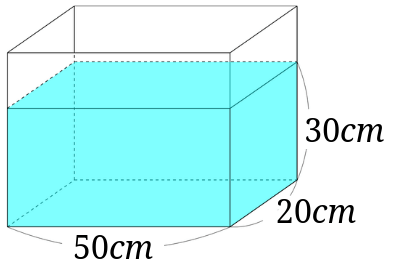
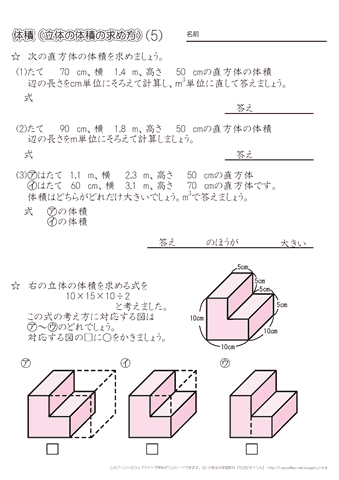
教え方4-① 大きな直方体や立方体の体積を計算して求める方法に気づかせ、 (立方メートル)の単位を教えます。 問題 下図の直方体の体積を求めましょう 直方体の体積は、たて×横×高さで求められるので、cmで表すと 300cm×400cm×0cm = となります。そうすると、例題の直方体の場合、縦・横に 3 3 個・ 4 4 個と並べているので 1 1 段に 12 12 個。 これを 5 5 段並べているので 12× 5=60 12 × 5 = 60 個だとわかります。 1cm3 1 c m 3 が 60 60 個なので、体積は 60cm3 60 c m 3 です。つまり、立方体は全部の辺の長さが同じなので、立方体の体積を求める公式は次のようになります。 「一辺」×「一辺」×「一辺」=体積 一つの辺の長さを3回かける と覚えるとおぼえやすいですね。
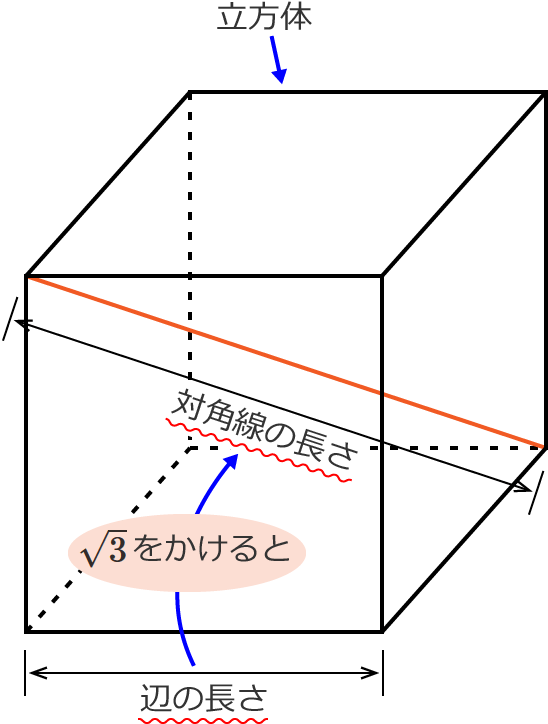
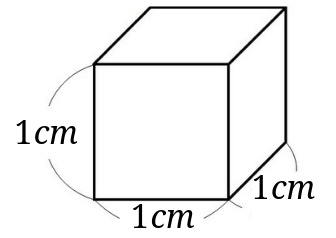
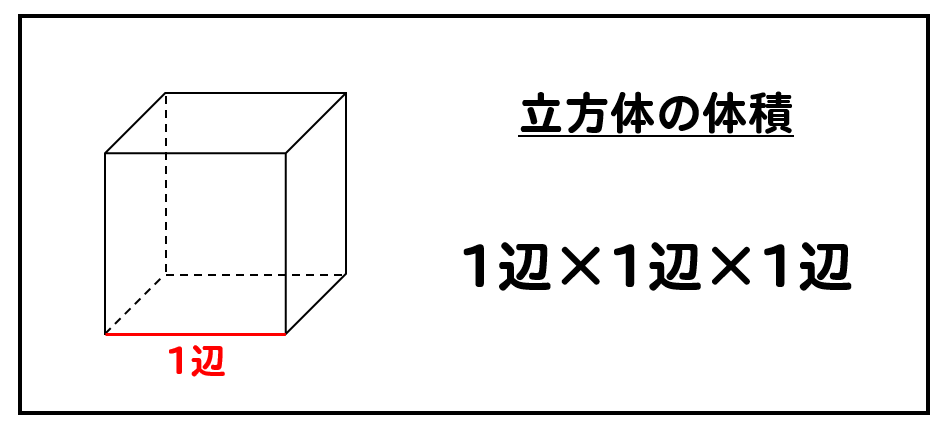
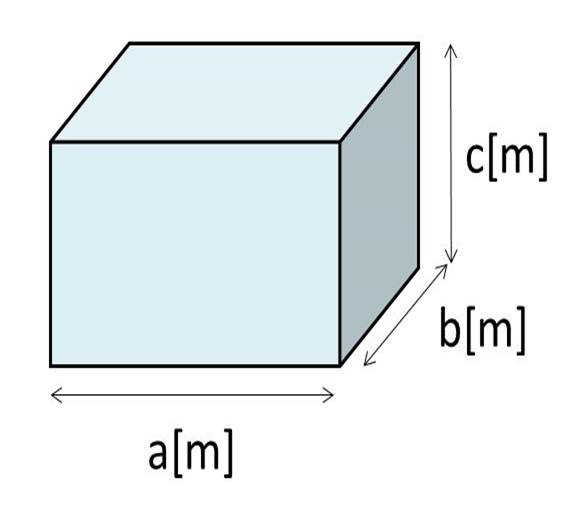
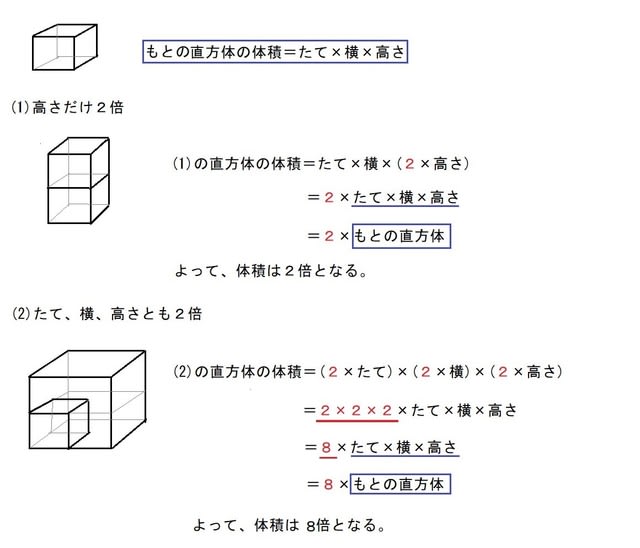
立方体の12の辺の長さは等しく、これを $a$ とします。立方体の体積 $V$ は、次の式で求められます。 立方体 (りっぽうたい) の体積 \begin{align*} V = a^3 \end{align*} 体積 = 一辺 × 一辺 × 一辺1辺が1cmの立方体何個分でしょうか。 1立方メートル 1辺が1mの立方体と同じ体積を、1立方メートルといい、 と表します。 立方メートルは、体積の単位です。 次に、1 は何 か考えましょう。 1m=100cm なので、 1m×1m×1m=1 は、 100cm×100cm×100cm= と角柱の体積は,直方体・立方体の体積の求め方を想起させ,次のような順序で考えを進め ながら学習していく。 ① 四角柱の体積は,高さ1㎝の四角柱が何個あるかわかれば求められる。
・立方体と直方体両方を問題としていた。 第2 時 ・公式は段階を経て導き出しているので分かりやすい。 第3 時 ・多少数字は違うが形はじである。 ・求め方を自分でよく考え、説明させる問題である。 第4 時 ・1 ㎥の立方体をつくって、量感を育てる。体積Vが8の立方体の1辺の長さ・表面積 1辺の長さ a:2 表面積 S:24 体積・表面積の計算 ・ 立方体の体積・表面積 ・ 立方体の体積から1辺 ・ 立方体の表面積から1辺 ・ 直方体の体積・表面積 ・ 直方体の1辺・表面積 立方体の体積は、次の公式で求められます。 立方体の体積=1辺×1辺×1辺 直方体の体積の求め方公式 直方体の体積は、次の公 読者になる



直方体や立方体の体積を求める応用問題の解き方は どうやって教えるといいの みけねこ小学校




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強
よって、求める表面積は、2×9π 48π=66π cm 2立方体(りっぽうたい)の体積は「1辺の長さの三乗」で計算します。 立方体は辺の長さが全て同じ立体図形です。 1辺が1cmのとき、全ての辺が1cmとなります。 体積の公式は「縦×横×高さ」です。 立方体の全ての辺は同じ長さなので、立方体の体積は「1辺の長さの三乗」です。 今回は立方体の体積の計算、単位、公式、求め方、リットルとの関係について説明し 立方体の体積の計算問題を解いてみよう それでは、立方体の体積の求め方に慣れるためにも計算問題を解いていきましょう。 ・例題3 1辺の長さが2cmの立方体の体積はいくらでしょうか。 ・解答3 上の立方体の体積の公式を元に計算していきます。




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学



5年算数体積2わかる教え方
ア 角柱および円柱の体積の求め方を考えること。 直方体,立方体の場合の体積の求め方をもとにして,これらの立体の体積も計算によって求める ことができることを理解することが主なねらいとなって1辺が 1 cm の立方体が何個分あるかで求めることができます。 縦×横×高さ=直方体の体積,1辺×1辺×1辺=立方体の体積となります。 実施時期た,「立方体及び直方体の体積の求め方」では,「直方体の体積」33/36 名(92%),「立方体の体積」34/36 名(94%)であった。直方体や立方体の体積の誤答は,全て計算ミスによるものだった。 算数科の授業においては,「全員が協力し合い,『できた



計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



石を水の入った水槽に沈めて体積を求める問題の教え方 みけねこ小学校
・立方体,直角柱 ・正方形,長方形の面積の求め方 5年生 ・図形の合同 ・角柱 ・三角形,平行四辺形の面積の求め方 ・立方体,直角柱の体積の求め方 6年生 ・角柱,円柱の体積の求め方 表1 表1を見ると,平面図形の四角形の学習では,立方体の体積 立方体の辺の長さ 直方体の体積 四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から)立方体 直方体 断面積から体積計算 公式 求め方 高さ 底面積 自動 volume




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書




体積 表面積
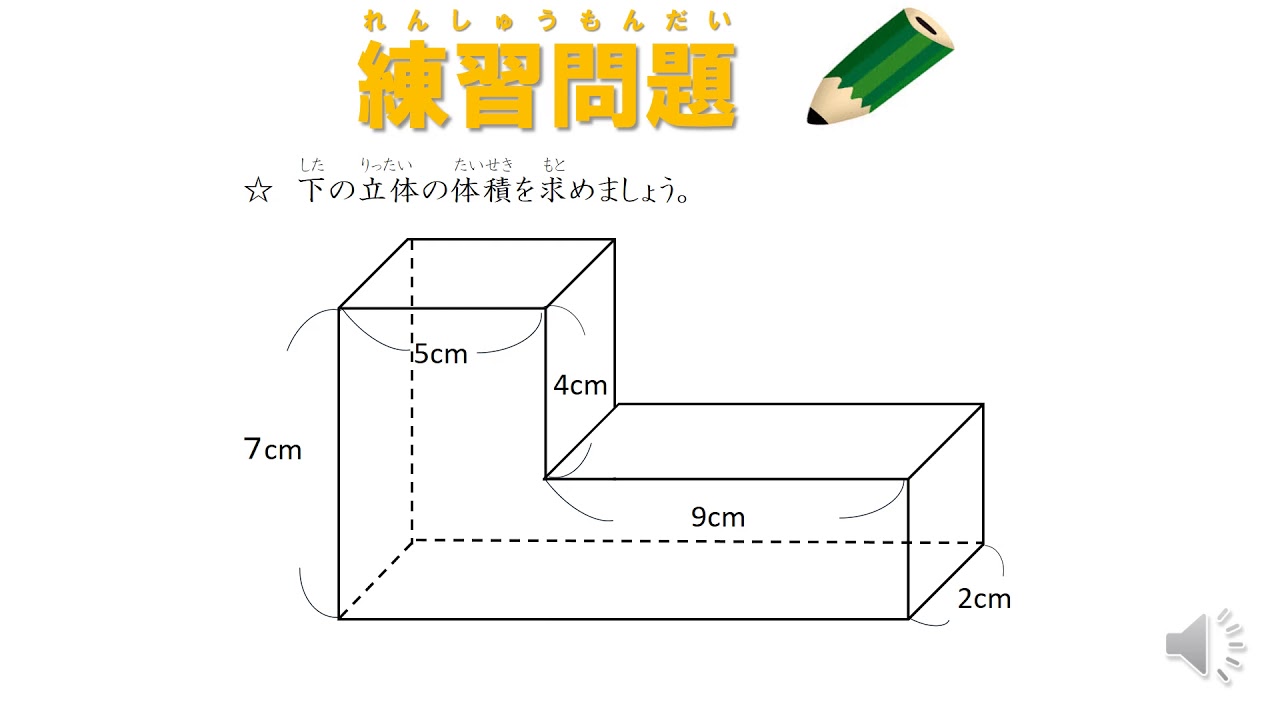
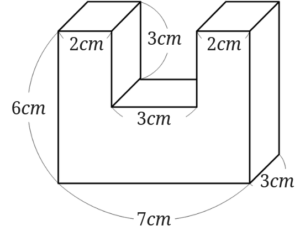
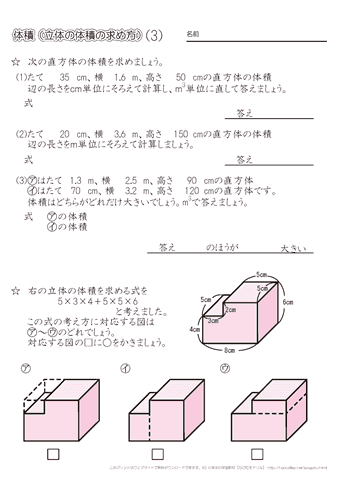
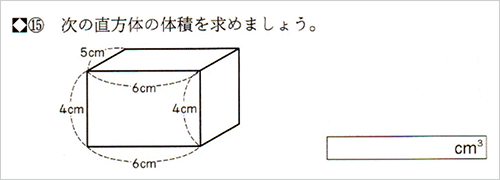
年 組 番 名前 524 直方体や立方体の体積 体積の求め方の工夫 下のような形の体積を求めます。 かのんの考え方で、体積を計算して求めましょう。もののかさの表し方を考えよう 課 問 練 ふ のような形の体積の求め方を考えよう。 のような形の体積も、直方体や立方 体の形をもとにして考えれば求めること ができる。 体積を求めましょう。 =325 答え 352㎤ 体積は何㎤ですか。 =294 答え 294㎤ 例題3)下の図の直方体ABCDEFGHにおいて、AB=6cm、AD=4cm、AE=4cmのとき、四面体ABCFの体積を求めなさい。 19 群馬県公立高校入試問題 22 例題3のポイントは、「四面体ABCFは三角錐だ!



小学算数 立体の体積の公式と単位 立方体 直方体 円柱 三角柱 偏差値40プログラマー




小5 直方体の体積 複雑な立体を求める 日本語版 Youtube
立方体の体積は (1辺)×(1辺)×(1辺) で求めることができます。 だけど、これは直方体の (たて)×(よこ)×(高さ) これと全く同じものです。 全ての辺が同じ長さになってしまう立方体では、辺の区別をつけずれらの求め方を考え、求 めようとしている。 既習の学習事項を基 に、辺の長さを用いた計 算によって体積が求め られることを考えてい る。 公式を用いて体積を 求めることができる。 単位と測定の意味や、 直方体や立方体の体積 の求め方を理解し、体積(イ)立方体及び直方体の体積の計算による求め方について知ること。 イ 次のような思考力,判断力,表現力等を身に付けること。 (ア)体積の単位や図形を構成する要素に着目し,図形の体積の求め方を考えるとともに,体




容積の求め方 小学生の算数質問ひろば 進研ゼミ小学講座




立体の体積を求める公式
ってことさ。 たとえば、下の辺が4cm、上の辺が2 cm、高さ6cmの正四角錐台ABCDEFGHがあったとしよう。 この立体の体積は、 1/3 h ( a^2 ab b^2 ) = 1/3 × 6 × ( 4^2 4 × 2 2^2) = 2 × ( 16 8 4 ) = 56 cm^3 になるよ! めんどい計算式だけど、




体積の求め方 立方体 長方体 小学生 算数のノート Clear




中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー



3




すきるまドリル 小学5年生 算数 体積 無料学習プリント すきるまドリル 無料学習プリント




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



立方体の対角線の長さの求め方
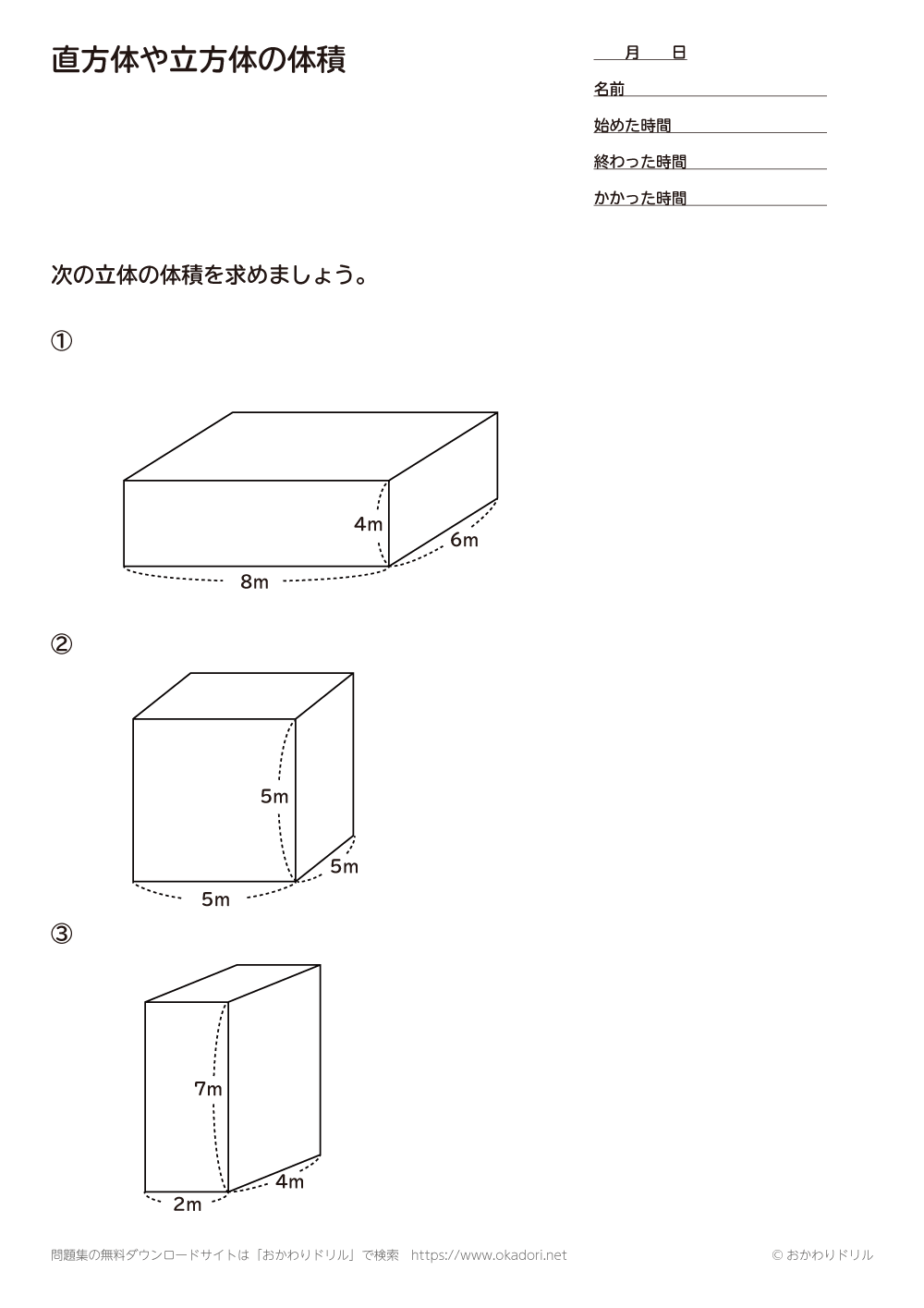



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




6年算数立体の体積1 教え方




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




体積の測定 測定のことを 即 知りたい ソクシリ キーエンス



Www Nagoya C Ed Jp School Shimizu E 5sansu A Pdf



体積 直方体と立方体のかさを表そう 第5学年 小学校 算数 My実践事例 日本文教出版



斜めに切った円柱や角柱の体積を求める方法 中学受験ー算数解き方ポータル




小5 複雑な立体の体積 直方体 日本語版 Youtube



立方体の公式は 1分でわかる意味 体積の公式と例題の求め方 表面積の公式



1



体積とは コトバンク



直方体や立方体の体積を求める公式は どうして たて 横 高さ なの みけねこ小学校



立方体の体積 小学生はどうやって問題解く 計算のやり方を解説 数スタ




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学



Www City Hadano Kanagawa Jp Www Contents Simple Kuukan291 Pdf



5 5 複雑な立体の表面積と面積を求めるには さんすうがく
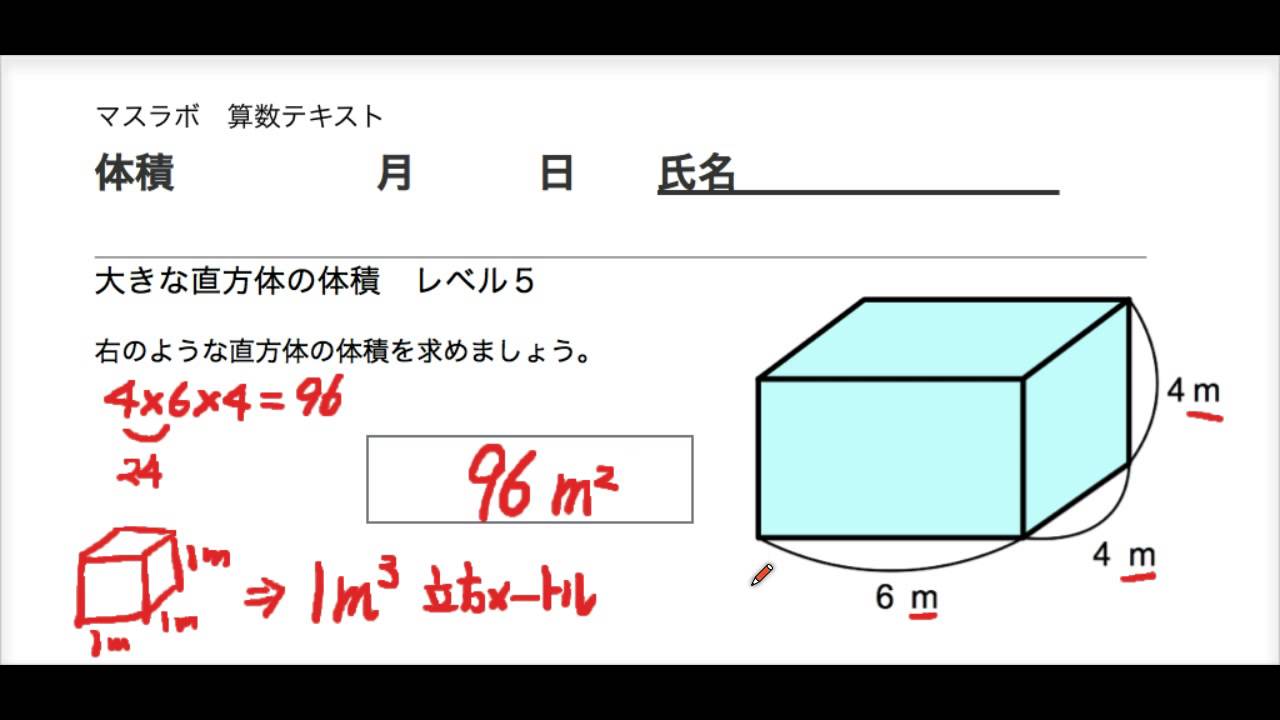



無料印刷可能 体積 容積 求め 方



Search Results For Page 312 横山験也のちょっと一休み




算数 円柱の体積の求め方 公式で確認 小学生向け 数スタ




体積の求め方 計算公式一覧




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
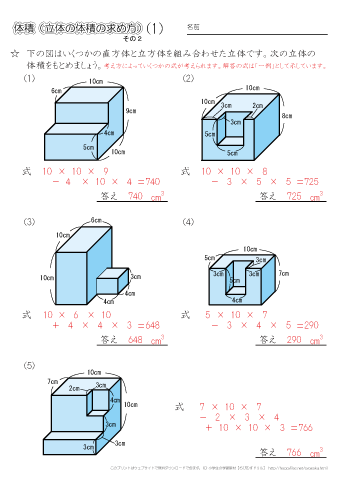



小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生



数学の問題教えてください 立方体から切り取った三角錐の体積はどうやって Yahoo 知恵袋




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




どうして1 3なの 錐の体積の公式の求め方 まなべーと




複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座




小学5年生の算数 動画 直方体と立方体の体積 の問題 19ch
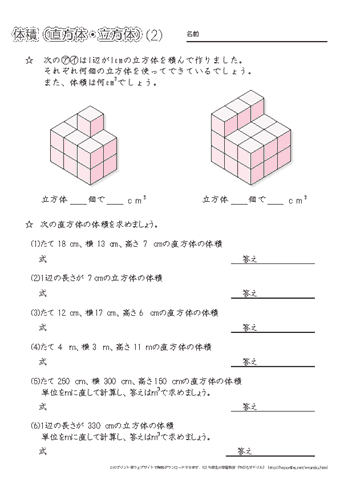



小学5年生の算数 体積 直方体と立方体の体積の求め方 練習プリント ちびむすドリル 小学生




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun




どうして1 3なの 錐の体積の公式の求め方 まなべーと




私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館




小5 算数 小5 3 直方体と立方体の体積 Youtube
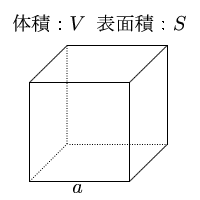



立方体の体積から1辺 体積 表面積の計算 計算サイト



立方体の公式は 1分でわかる意味 体積の公式と例題の求め方 表面積の公式



地図の体積計測




体積の求め方 計算公式一覧



Excel エクセルで立方体 直方体の体積の計算を行う方法 立方メートル 白丸くん




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




直方体 立方体の体積 Youtube



私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館



1




角柱の体積の公式 求め方は底面積と高さに注目するだけだ 中学や高校の数学の計算問題




四角錐台の体積 高精度計算サイト



5年算数体積2わかる教え方




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生



一辺が12cmの立方体の中にある三角錐の体積の求め方を教えてく Yahoo 知恵袋



算数科予習プリント 体積の求め方は考えられたかな 翁島 おきなしま 小学校ホームページ




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット



直方体 立方体の体積 小5 きちんと式を書けば簡単 算数の教え方教えますmother S Math Happy Study Support




面積や体積のかけ算の順序 おかしな算数教育 身勝手な主張



体積の応用




体積の求め方 計算公式一覧




立方体や直方体の体積の求め方を習ったら 少し応用的な問題にも取り組みましょう 展開図を見て 体積を求める問題や いくつかの立方体や直方体の面積を足したり引いたりして解く問題です 学習ノート 小学校 算数 学習




算数 新 小5編 体積 小4から始める高校受験 お母さん 一緒にがんばりましょう




小5 算数 小5 5 体積の求め方のくふう Youtube



兵庫県実践事例 算数小学校6年



算数流体積の求め方 Sciencelab 冨田塾



中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー




体積 上 体積の意味から 立方体 直方体 柱 錐の体積の求め方 思考力算数練習張シリーズ 46 エム アクセス 本 通販 Amazon



栃木県総合教育センター 算数 数学 学びの杜 小学校6年生 算数 体積のはかり方と表し方




世界一分かりやすい算数 小5 体積
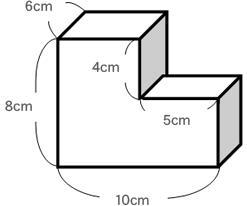



体積 直方体と立方体のかさを表そう 第5学年 小学校 算数 My実践事例 日本文教出版



5年算数体積2わかる教え方
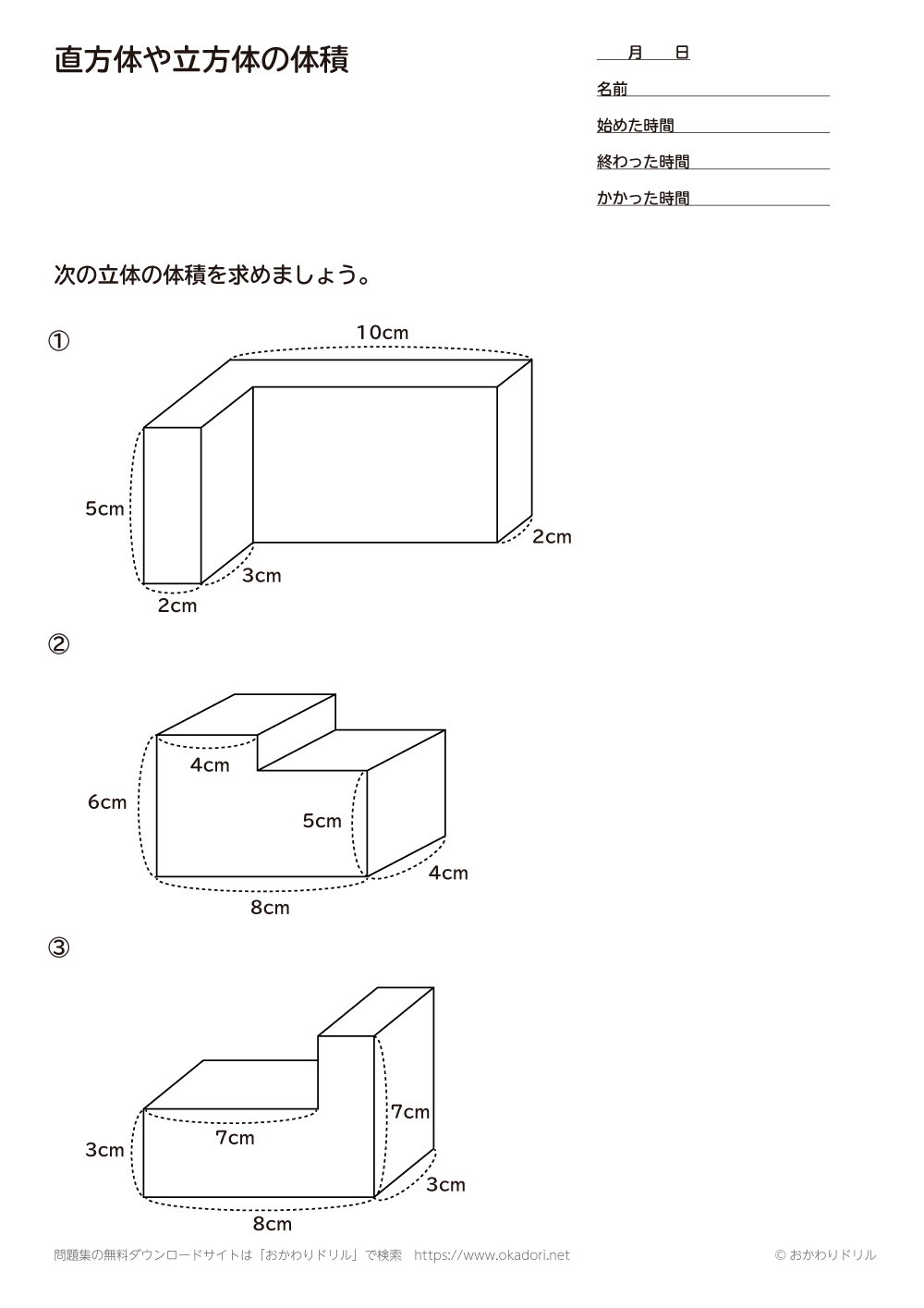



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル
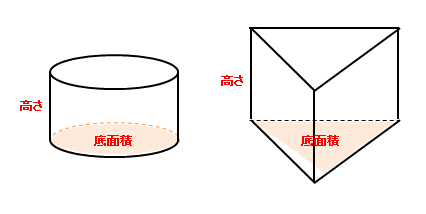



小学算数 立体の体積の公式と単位 立方体 直方体 円柱 三角柱 偏差値40プログラマー
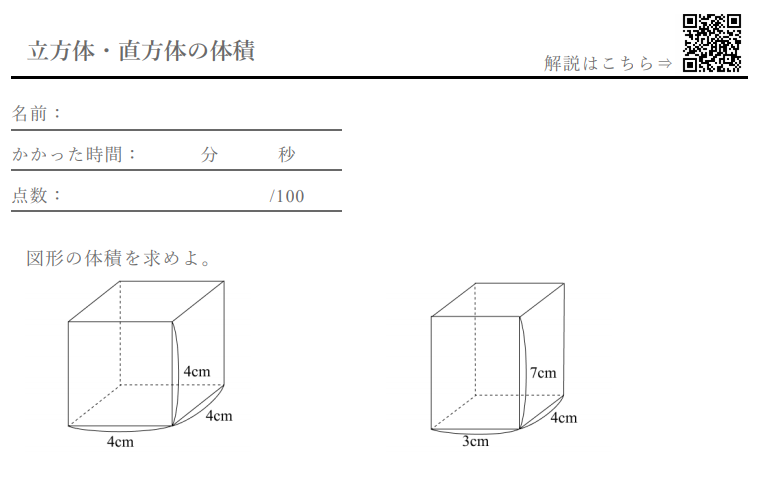



立方体 直方体 の体積 計算ドリル 問題集 数学fun



体積の公式は 1分でわかる求め方と覚え方 一覧 三角柱 円柱 三角錐の体積



6年算数立体の体積1 教え方




マスラボ 小学校5年 体積 レベル3 立方体の体積の求め方 Youtube
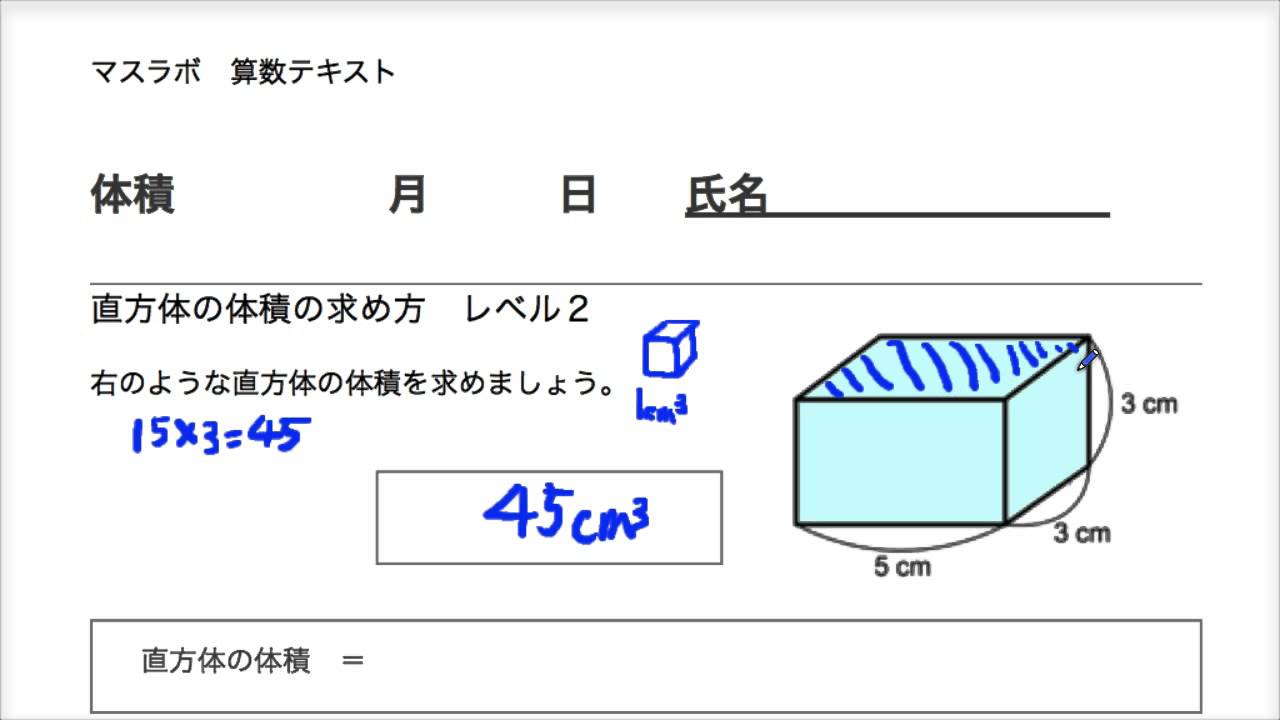



マスラボ 小学校5年 体積 レベル2 直方体の体積の求め方 Youtube




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




多くの教師が失敗する角柱の体積の求め方 算数を究める



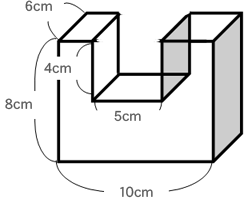
この立体の体積の求め方を分かりやすく説明つきで教えて下さい Yahoo 知恵袋




超簡単 体積の求め方 苦手な数学を簡単に
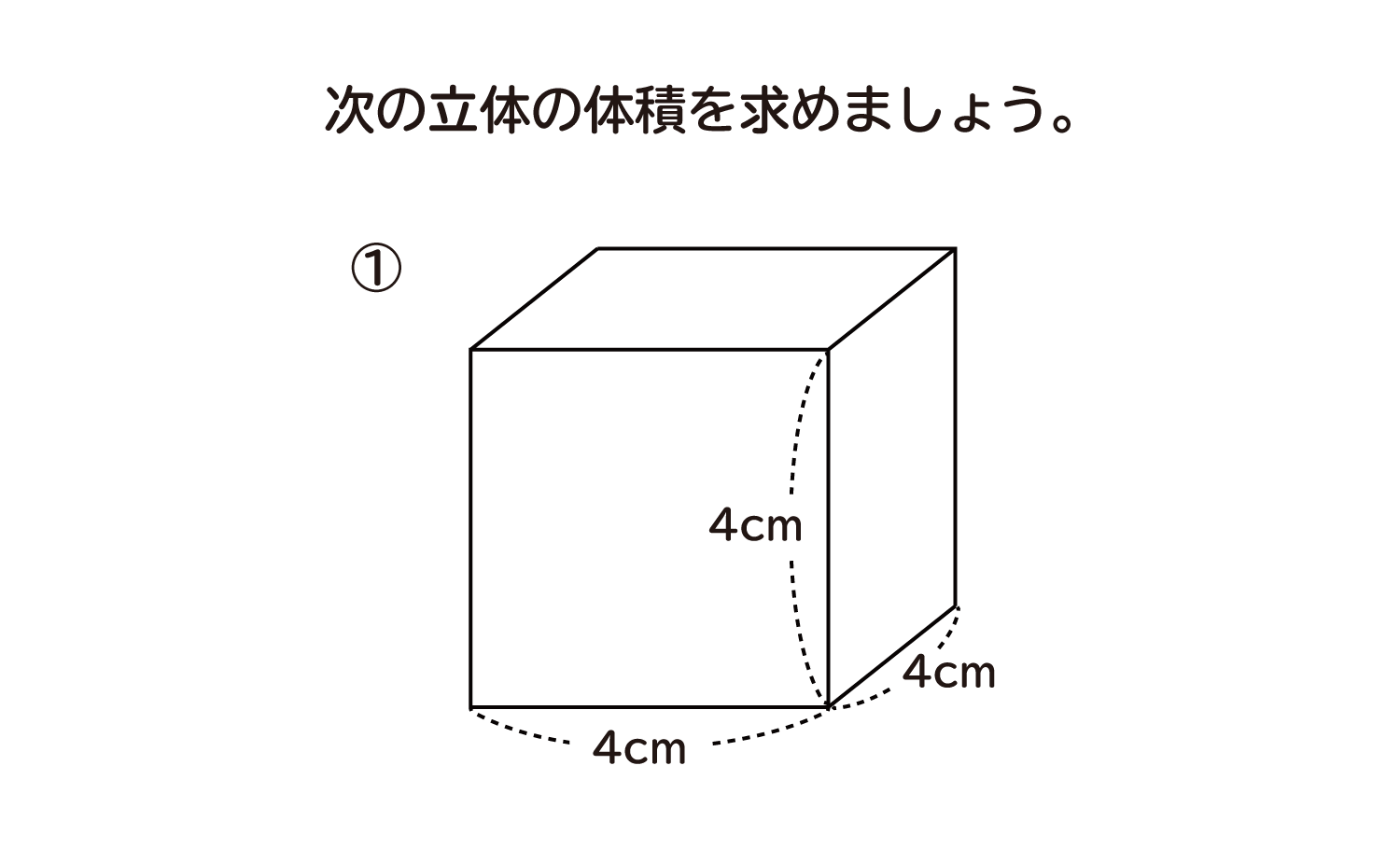



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル
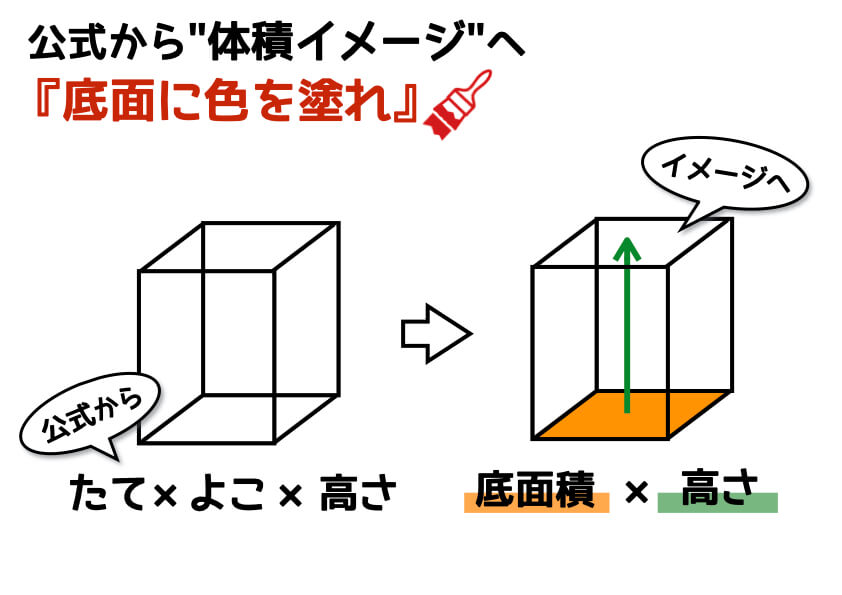



小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ



1



体積計算機 断面積から体積計算 公式 求め方




体積の求め方 計算公式一覧



0 件のコメント:
コメントを投稿